7月 25 2018
個数演算子を眺めながら・・・
個数演算子は場の量子論に登場する演算子のことで、簡単に言うと、波動化した場を粒子として表現する数学的手法のようなものだ。
個数演算子には粒子を生成させる演算子である生成演算子と、粒子を消滅させる演算子である消滅演算子という二種類の演算子がある。先日話したヒルベルト空間で構成される場|Ψ>にこれらの演算子を作用させることによって、粒子を作り出したり、消したりすることができる―とされている。
興味がある方はネットなどで調べてみればいいと思うが、ヌーソロジーの複素空間認識の思考で、この生成消滅演算子の本質的な意味をイメージしていくと、これはすごく単純なことを言っているのではないかと思われてくる。つまり・・・。
「意識が後ろ=a†で世界を構成してしまうと、前=aが粒子になって現れるよ」と言ってるように聞こえる。
もう少し説明してみよう。
「わたし」がグルっと周囲を見回したとき、普通それは時空の広がりとして現れるよね。これは、いつも言ってるように、他者に「見られる」ことによって生まれている空間だから、肉体的自我に囚われた我執の空間と言ってもよいものなのね。しかし、そのとき同時に、「見る」ことが起こっている奥行きそのものの空間もグルって回ってる。こちらは、昨日説明したように、ヒルベルト空間として「前」で丸まってる。このヒルベルト空間が一個の物質粒子に当たると思うといい。
要は、「後ろ」によって支配されたマクロの空間認識の中で、「前」は人知れずミクロとして沈み込んでいるというわけだ。ハイデガー風に言うなら、これは隠蔽された「存在」と言っていいものになる。流れる時間のその瞬間の隙間に本来的時間である純粋持続=永遠が入り込んでるってわけ。
物理学や哲学に不慣れな人には、やたら難しいことをこねくりまわしているように見えるかもしれないけど、ヌーソロジーはこの隠蔽のヴェールを取り去る作業(霊の顕現)を人間の理性に了解可能な形で行っていると考えてほしい。
この作業が成功すれば、すべての素粒子は消滅演算子(本来的自己の覚醒を意味する)のもとにその姿を消していくことになるんじゃないかな。
この数式からは、そうしたニオイがプンプン漂ってる。

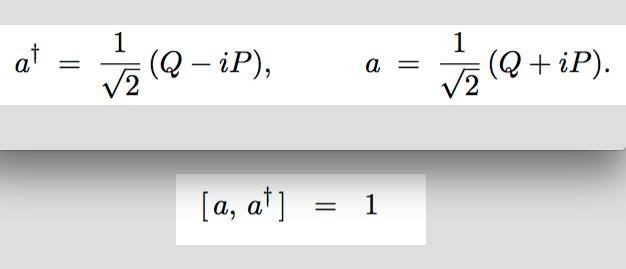






2019年11月25日 @ 06:35
√2がでてくるということは、直交座標系において座標軸間を横切る斜線のことを表現していると推測できるのではないか?ピタゴラスの定理
A^2 +B^2=C^2
のこと。
直交座標系を虚軸と実軸の複素数平面とすれば、生成演算子・消滅演算子とは、虚軸から実軸へ、実軸から虚軸への変換のことであり、虚・実の回転運動における加速度のことになるのではないか。こうイメージすると、実にスッキリして分かり易い気がするのだが。
2019年11月28日 @ 13:13
虚軸と実軸というより、上半平面と下半平面の関係になります。
ヌース的解釈では前方と後ろです。
自他のあいだで、両者が捻れています。
それを掛け算し合って、粒子を出現させたり、消去したりしています。