4次元と3次元の関係性

数的神秘学の系譜は「3」と「4」を宇宙の成り立ちの根本的要素と見なします。かのヨハネス・ケプラーと神聖幾何学者ロバート・フラッドの間でも「3と4のどちらが神聖か」を巡って論争したこともありました。このことは空間にもダイレクトに反映されています。すぐに直感されるのは3次元と4次元の関係ですね。
　
19世紀末から20世紀初頭にかけて「四次元思想」というものが大流行しました。これは心の世界を4次元空間とみなして、人間の知性を物質的思考から解放していこうとする思想でした。その先駆けを作ったのがチャールズ・ヒントンという人物です。『フラット・ランド』などが有名です。
　
ヒントン以降の伝統として、多くの人は空間の次元を思考する場合、0次元を点、1次元を線、2次元を面（正方形）、3次元を立体（立方体）、4次元を超立体（4次元立方体）というように帰納的に思考していこうとします。しかし、こうした思考法は4次元を延長空間として仮定しているようなもので、そこで比喩的に類推されてくる図形はほとんど意味を持ちません。というのも、いつも言っているように実際の4次元空間とは持続空間として働いているからです。
　
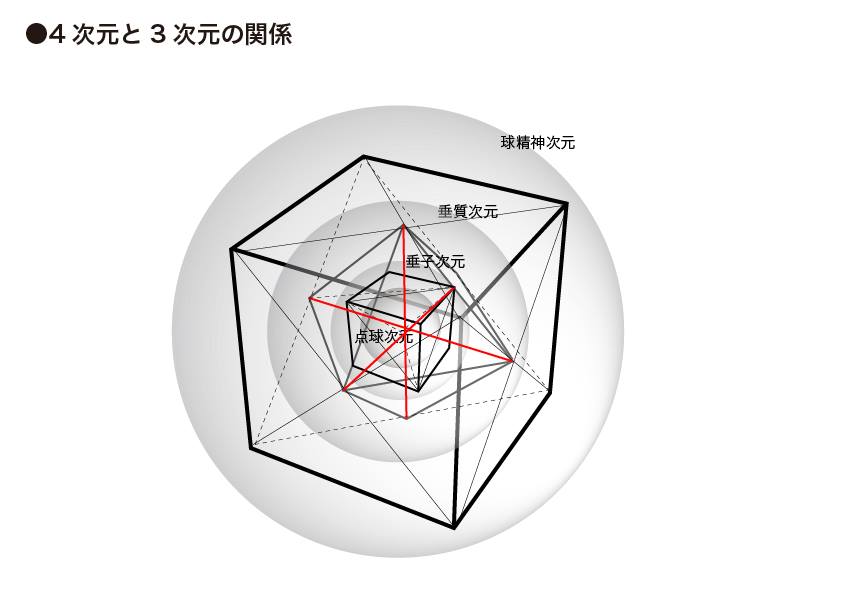
ですから、4次元は3次元では影としてしか図形化できないと考える必要があります。そして、その4次元が3次元に等角写像として現れたものが正四面体なんですね。
　
正四面体はそれ自身が点と面の関係において双対となっていますが、この双対関係を反転させたもう一つの正四面体を組み合わせるとケプラーの星形八面体ができます。いわゆるスピ系で「マカバ」と呼ばれている立体図形です。このとき二つの正四面体の交差する部分に正八面体が現れますが、この正八面体が3次元のイデアに相当すると考えるといいのではないかと思います。
　
同時にこの双対の正四面体の合計八つの頂点を結ぶと正六面体=立方体が現れます。このことは立方体が4次元の双対空間を表す図形であることを意味しています。つまり、マカバ図形とは二つの4次元から一つの3次元が作り出されてくる仕組みを表現していると考えて下さい。
　
これは、立方体を3次元の象徴的な図形として見ること自体が誤りだということを意味しています。
　
マカバを基礎として出現する正六面体と正八面体の内接・外接関係は極めて重要です。ほんとうの意味での「次元」、つまり、持続空間が作り出している次元とは、この内接・外接の反復性によって形作られています。