次回のヌースレクチャーでは現代物理学の話をしようと思います。おそらく、ヌーソロジーから見た素粒子空間の話がメインになるでしょう。
現代物理学は物質の大本の構成要素を素粒子と見なしているわけですが、ここには相変わらず、素粒子を対象として見なす認識の型が働いています。OCOT情報のいう人間型ゲシュタルトというやつですね。
波動関数ψ(x,t)という複雑な数式で表現されている様々な素粒子の有様(ありよう)も、相変わらず「観察される対象」であって、それは、それらの数式が時間tと空間xをパラメーターとして関数化されているところにも表れています。対象は、たとえどんな運動をしていようとも、常に時間と空間の中になければならない、とする考え方です。
しかし、素粒子は、観測問題などで取り沙汰されているように、普通の対象とは全く別の性質を持ったものです。何らかのかたちで観測者を巻き込んだ形で存在しているんですね。観測問題というのは、本来、波動関数ψ(x,t)の状態で存在している素粒子が、人間の観測が波動関数の崩壊を起こす原因となっていて、それによって、はじめて測定値がある値に定まるというものです。
この「観測」ですが、これは、数学的には「波動関数ψ(x,t)の微分」という形で表されていると考えることができます。たとえば、運動量の導出は波動関数ψ(x,t)を位置xで微分することによって、エネルギーであれば、同じく波動関数ψ(x,t)を時間tで微分すると出てきます。しかし、波動関数ψ(x,t)自体は指数関数の形をしているので、微分しても常に元の関数は残されて、導き出された物理量に対して、常に位相因子としてくっついてきます。
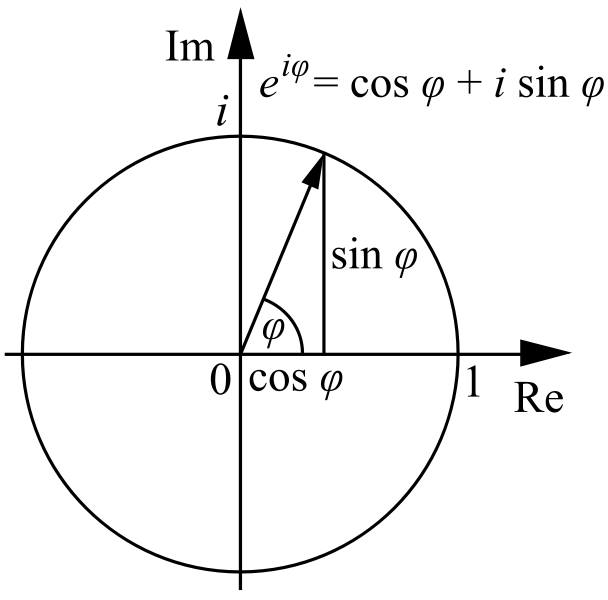
分かりやすく言えば、計算によって素粒子の運動量やエネルギーが導き出されたとしても、そこに、つねにψ(x,t)がくっついていて、複素平面上の回転として表される何かがグルグルと回っているわけです。このグルグルは、現在、物理学では「確率の変動」として解釈されています。たとえ、運動量pが導き出されたとしても、それは確率的にしか把握されない、というわけです。これは位置xにしても、エネルギーEにしても、同じです。
波動関数ψ(x,t)に対するこうした確率解釈から、物質は確率的存在でしかないという言説が生まれ、それが宇宙全体に拡大解釈されて、並行宇宙仮説なんかが出てきています。この仮説は現在のスピ系の思想や哲学系の思想にもかなり影響を与えていますよね。宇宙は選択によってその瞬間、瞬間に分岐してるとか、非共可能的次元の世界が存在するとか、いろいろですが。
でも、個人的には、この確率解釈は、物理学が時間と空間を先行させて、そこに実在の形式を見ているために生まれている誤った解釈のように思えます。つまり、わたしたちが実在と見なしているような宇宙が、無数、枝分かれしたような別の宇宙などといったものは存在しない、ということです。ヌーソロジーの観点からから見ると、この確率は、むしろ、時間と空間が認識に生じる以前の、人間個々の想像力のフィールドで生まれている「共可能的次元」の表現です。
この共可能的次元が、自己の内部次元、さらには、自己-他者間で、総合化されていくことによって(物理学的には対称性の拡張に当たります、)時間と空間という、自他の間で相互了解が取れる客観的実在の場所が認識に生じてくる、という仕組みになっていると考えています。
いずれにしろ、ヌーソロジーの思考から見ると、素粒子世界というのは、ドゴン族のいう〈先導記号〉のごときものであるということですね。わたしたちの世界に対する認識を可能にさせている、哲学の言葉でいうなら〈超越論的構成〉を持った幾何学構造体です。
今回のレクチャーでは、こうした観点から、素粒子世界を貫いているシステムを、奥行きと幅の差異の概念をベースに具体的に説明してみようかな、と思っています。
位置空間と運動量空間の反転関係、確率解釈、波動関数の崩壊、スピン1/2空間、など、素粒子世界が内在させている様々なナゾの解明に観察子の概念がいかに有用かが、参加された皆さんにも、かなり伝わることでしょう。
いや、全然、伝わらなかったりもして(笑)







11月 19 2014
ヌーソロジーの素粒子論
次回のヌースレクチャーでは現代物理学の話をしようと思います。おそらく、ヌーソロジーから見た素粒子空間の話がメインになるでしょう。
現代物理学は物質の大本の構成要素を素粒子と見なしているわけですが、ここには相変わらず、素粒子を対象として見なす認識の型が働いています。OCOT情報のいう人間型ゲシュタルトというやつですね。
波動関数ψ(x,t)という複雑な数式で表現されている様々な素粒子の有様(ありよう)も、相変わらず「観察される対象」であって、それは、それらの数式が時間tと空間xをパラメーターとして関数化されているところにも表れています。対象は、たとえどんな運動をしていようとも、常に時間と空間の中になければならない、とする考え方です。
しかし、素粒子は、観測問題などで取り沙汰されているように、普通の対象とは全く別の性質を持ったものです。何らかのかたちで観測者を巻き込んだ形で存在しているんですね。観測問題というのは、本来、波動関数ψ(x,t)の状態で存在している素粒子が、人間の観測が波動関数の崩壊を起こす原因となっていて、それによって、はじめて測定値がある値に定まるというものです。
この「観測」ですが、これは、数学的には「波動関数ψ(x,t)の微分」という形で表されていると考えることができます。たとえば、運動量の導出は波動関数ψ(x,t)を位置xで微分することによって、エネルギーであれば、同じく波動関数ψ(x,t)を時間tで微分すると出てきます。しかし、波動関数ψ(x,t)自体は指数関数の形をしているので、微分しても常に元の関数は残されて、導き出された物理量に対して、常に位相因子としてくっついてきます。
分かりやすく言えば、計算によって素粒子の運動量やエネルギーが導き出されたとしても、そこに、つねにψ(x,t)がくっついていて、複素平面上の回転として表される何かがグルグルと回っているわけです。このグルグルは、現在、物理学では「確率の変動」として解釈されています。たとえ、運動量pが導き出されたとしても、それは確率的にしか把握されない、というわけです。これは位置xにしても、エネルギーEにしても、同じです。
波動関数ψ(x,t)に対するこうした確率解釈から、物質は確率的存在でしかないという言説が生まれ、それが宇宙全体に拡大解釈されて、並行宇宙仮説なんかが出てきています。この仮説は現在のスピ系の思想や哲学系の思想にもかなり影響を与えていますよね。宇宙は選択によってその瞬間、瞬間に分岐してるとか、非共可能的次元の世界が存在するとか、いろいろですが。
でも、個人的には、この確率解釈は、物理学が時間と空間を先行させて、そこに実在の形式を見ているために生まれている誤った解釈のように思えます。つまり、わたしたちが実在と見なしているような宇宙が、無数、枝分かれしたような別の宇宙などといったものは存在しない、ということです。ヌーソロジーの観点からから見ると、この確率は、むしろ、時間と空間が認識に生じる以前の、人間個々の想像力のフィールドで生まれている「共可能的次元」の表現です。
この共可能的次元が、自己の内部次元、さらには、自己-他者間で、総合化されていくことによって(物理学的には対称性の拡張に当たります、)時間と空間という、自他の間で相互了解が取れる客観的実在の場所が認識に生じてくる、という仕組みになっていると考えています。
いずれにしろ、ヌーソロジーの思考から見ると、素粒子世界というのは、ドゴン族のいう〈先導記号〉のごときものであるということですね。わたしたちの世界に対する認識を可能にさせている、哲学の言葉でいうなら〈超越論的構成〉を持った幾何学構造体です。
今回のレクチャーでは、こうした観点から、素粒子世界を貫いているシステムを、奥行きと幅の差異の概念をベースに具体的に説明してみようかな、と思っています。
位置空間と運動量空間の反転関係、確率解釈、波動関数の崩壊、スピン1/2空間、など、素粒子世界が内在させている様々なナゾの解明に観察子の概念がいかに有用かが、参加された皆さんにも、かなり伝わることでしょう。
いや、全然、伝わらなかったりもして(笑)
By kohsen • 01_ヌーソロジー • 0 • Tags: 波動関数, 素粒子