
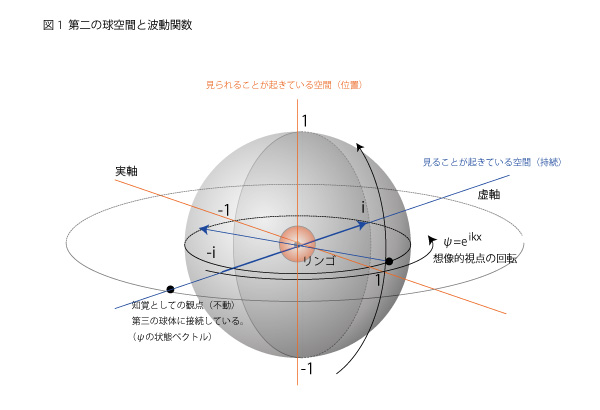
わたしたちの内在性は空間の無限の多層性によって構成されている。この多層性はレイヤーのように重なり合う性質を持っているのだけど、その重なりの母胎となる空間を数学的に表現したものがおそらく複素2次元空間だ。この複素2次元空間は実2次元、虚2次元よりなる4次元の空間だが、ここでいう実2次元とは知覚正面としての2次元平面であり、虚2次元とは自己と他者の視線から構成されている2次元である。この複素2次元空間と前回紹介した球空間モデルに沿って、今日は第二の球空間が持つ意味について簡単に説明してみよう(下図1参照)。
目の前にリンゴがある。目を閉じてそれを触ってみる。その手触りを通してひんやりとした冷たさとスルスルしたリンゴ表面の感覚が触覚を通じて内在性に伝わってくる。しかし、目を閉じた状態ではリンゴが球体であるという認識は生まれてはいない。当然、触っているだけなのだから、そこにリンゴを象る外部が存在しないためだ。そこに感じられるのは何らかのかさばりの感覚のみであって、触覚は一途にリンゴの内部性をそのかさばりにおいて指向している。これが第一の球体だ。
僕らの意識にリンゴの外部が出現するのは目を開いたときだ。そこにはリンゴの視像を円形に象るリンゴの背景空間が用意されている。こうして図(リンゴの視像)と地(背景空間)の差異によってリンゴの象りがクリアに認識されてくる。しかし、触覚と視覚だけでは「リンゴが球体である」いう認識は生まれてはこない。リンゴが球体として見えだすためには、「リンゴの周りのいろいろな視点からリンゴが見える」という準観察力、つまり想像力(サルトル)が働かなくてはならない。20世紀の初めにキュビストたちが探求したモノのほんとうの姿がある場所で働いている力のことだ。
この想像力は自分の意識を確かめてみればすぐに分かるように、観察の視点がリンゴの周りをグルグルと回ることで成り立っている。眺める角度も自由、距離も自由。こうした想像力を内在性に提供しているのがここで示した第二の球体の働きだと思ってもらえばいい。こうした視線は想像なのだから、自分の知覚による視線というよりは、他者視線の借用により成り立っている。僕がもしあそこにいたなら、リンゴはこれこれあのように見えるだろうと、という想像を他者視線を使って想像しているのだ。それらの回転を観察しているのは、当然、実際の知覚としての視線である。
こうした様々な角度に想像の位置を移す回転は複素平面上の回転の合成で表すことができるが、この合成が実は物理学的には光子(電磁場)と同じ構造を持っている。準観察による観察視点はリンゴの周囲を絶えず旋回しているが、この意識の自由度を保証するグルグルが時空側に投げ出され、それが数学的に表現されているのが光子の波動関数(ψ=e^ikx)だ。この波動関数は想像が知覚の場へと落とされる瞬間にグルグルグルグルグルドッカーンと崩壊する。つまり、回転がストップしてしまう。これが波動関数の崩壊、つまり、観察行為そのものを意味することになる。
普通、物理学では波動関数(位相因子)の解釈として確率解釈が常識になっているのだが、それは物理学が粒子をあくまでも物質的実体として見なそうとしているからだと考えるといい。それに固執していると物質の正体は亡霊のようなものになってとらえどころのないものと化してしまう。この確率解釈は現象論的には正しいと言えるが、背後で活動しているこうした内在空間の構造を考えた場合、実はほとんど意味を為していない。
「モノが確率1としてここにある」ということの実質的意味を考えてみるといい。それは目の前に現前しているモノが騙し絵としてここにあるのではなく、ちゃんと触れて、3次元的に様々な角度からの見えを持って存在していることを意味するのだから、波動関数というのはむしろ、その確率「1」として確と存在しているモノの位置を裏で補完している当のものとしての役割を果たしていると考えなくちゃいけない。そうした裏の立役者である作用をモノ(粒子)として考えているから「確率的存在」などといった奇妙な解釈が生まれてくる。
ここで「確率」と呼ばれているものが意味している本質は次のような喩えで十分理解できるのではないかと思う。一本のボールベンを目の前で水平に持ち、それをゆっくり回してみよう。すると、ボールベンの視像は段々と短くなって、視線方向にボールペンが向いたときは長さが消える。そして、また段々と長くなってくる。この繰り返しだ。最も長く見えるときを確率「1」とすれば、消えるときが確率「0」になる。物理学が粒子の位置の確率振動と呼んでいるものはこのようなボールペンの長さの変化のようなものにすぎない。つまり、これは準観察として回転している視線から見える空間の幅を知覚の位置から見ている様子を表しているということだ。反対に回転する視線の方をボールペンに喩えれば、粒子の運動量の確率振動となる。位置とは幅、運動量とは奥行きの次元なのだ。
こうした回転が生じている空間は当然のことながら潰された奥行きを基盤とする持続空間の中で作られている。だから時空上ではそれはモノの内部に入り込み、ミクロ世界で活動しているかのように見える。創造物を享受する眼差しが、その虚軸的性質をうまく使って、再び、創造物の基盤の中へと回り込むという存在の円環性。この円環性が垣間見えたときに、世界が内在の環で繋がれるいることの直観が生まれてくる。精神と物質は物質の根源で繋がっているのだ。そして、その繋がりの覚知から世界の修復が開始されることになる。
こう考えると、その瞬間、瞬間で世界が枝分かれしていくというエヴァレットなんかが提唱している平行宇宙の考え方がいかに馬鹿げたものであるかが分かるだろう。こうした宇宙観は物質のみを実在と考え、見るものとしての内在性を忘却した思考が生み出した完全なフィクションである。信じてはいけない。それこそ宇宙がバラバラに崩壊していくことになる。







2月 6 2013
光子の波動関数とグルグルグルグルドッカーン
わたしたちの内在性は空間の無限の多層性によって構成されている。この多層性はレイヤーのように重なり合う性質を持っているのだけど、その重なりの母胎となる空間を数学的に表現したものがおそらく複素2次元空間だ。この複素2次元空間は実2次元、虚2次元よりなる4次元の空間だが、ここでいう実2次元とは知覚正面としての2次元平面であり、虚2次元とは自己と他者の視線から構成されている2次元である。この複素2次元空間と前回紹介した球空間モデルに沿って、今日は第二の球空間が持つ意味について簡単に説明してみよう(下図1参照)。
目の前にリンゴがある。目を閉じてそれを触ってみる。その手触りを通してひんやりとした冷たさとスルスルしたリンゴ表面の感覚が触覚を通じて内在性に伝わってくる。しかし、目を閉じた状態ではリンゴが球体であるという認識は生まれてはいない。当然、触っているだけなのだから、そこにリンゴを象る外部が存在しないためだ。そこに感じられるのは何らかのかさばりの感覚のみであって、触覚は一途にリンゴの内部性をそのかさばりにおいて指向している。これが第一の球体だ。
僕らの意識にリンゴの外部が出現するのは目を開いたときだ。そこにはリンゴの視像を円形に象るリンゴの背景空間が用意されている。こうして図(リンゴの視像)と地(背景空間)の差異によってリンゴの象りがクリアに認識されてくる。しかし、触覚と視覚だけでは「リンゴが球体である」いう認識は生まれてはこない。リンゴが球体として見えだすためには、「リンゴの周りのいろいろな視点からリンゴが見える」という準観察力、つまり想像力(サルトル)が働かなくてはならない。20世紀の初めにキュビストたちが探求したモノのほんとうの姿がある場所で働いている力のことだ。
この想像力は自分の意識を確かめてみればすぐに分かるように、観察の視点がリンゴの周りをグルグルと回ることで成り立っている。眺める角度も自由、距離も自由。こうした想像力を内在性に提供しているのがここで示した第二の球体の働きだと思ってもらえばいい。こうした視線は想像なのだから、自分の知覚による視線というよりは、他者視線の借用により成り立っている。僕がもしあそこにいたなら、リンゴはこれこれあのように見えるだろうと、という想像を他者視線を使って想像しているのだ。それらの回転を観察しているのは、当然、実際の知覚としての視線である。
こうした様々な角度に想像の位置を移す回転は複素平面上の回転の合成で表すことができるが、この合成が実は物理学的には光子(電磁場)と同じ構造を持っている。準観察による観察視点はリンゴの周囲を絶えず旋回しているが、この意識の自由度を保証するグルグルが時空側に投げ出され、それが数学的に表現されているのが光子の波動関数(ψ=e^ikx)だ。この波動関数は想像が知覚の場へと落とされる瞬間にグルグルグルグルグルドッカーンと崩壊する。つまり、回転がストップしてしまう。これが波動関数の崩壊、つまり、観察行為そのものを意味することになる。
普通、物理学では波動関数(位相因子)の解釈として確率解釈が常識になっているのだが、それは物理学が粒子をあくまでも物質的実体として見なそうとしているからだと考えるといい。それに固執していると物質の正体は亡霊のようなものになってとらえどころのないものと化してしまう。この確率解釈は現象論的には正しいと言えるが、背後で活動しているこうした内在空間の構造を考えた場合、実はほとんど意味を為していない。
「モノが確率1としてここにある」ということの実質的意味を考えてみるといい。それは目の前に現前しているモノが騙し絵としてここにあるのではなく、ちゃんと触れて、3次元的に様々な角度からの見えを持って存在していることを意味するのだから、波動関数というのはむしろ、その確率「1」として確と存在しているモノの位置を裏で補完している当のものとしての役割を果たしていると考えなくちゃいけない。そうした裏の立役者である作用をモノ(粒子)として考えているから「確率的存在」などといった奇妙な解釈が生まれてくる。
ここで「確率」と呼ばれているものが意味している本質は次のような喩えで十分理解できるのではないかと思う。一本のボールベンを目の前で水平に持ち、それをゆっくり回してみよう。すると、ボールベンの視像は段々と短くなって、視線方向にボールペンが向いたときは長さが消える。そして、また段々と長くなってくる。この繰り返しだ。最も長く見えるときを確率「1」とすれば、消えるときが確率「0」になる。物理学が粒子の位置の確率振動と呼んでいるものはこのようなボールペンの長さの変化のようなものにすぎない。つまり、これは準観察として回転している視線から見える空間の幅を知覚の位置から見ている様子を表しているということだ。反対に回転する視線の方をボールペンに喩えれば、粒子の運動量の確率振動となる。位置とは幅、運動量とは奥行きの次元なのだ。
こうした回転が生じている空間は当然のことながら潰された奥行きを基盤とする持続空間の中で作られている。だから時空上ではそれはモノの内部に入り込み、ミクロ世界で活動しているかのように見える。創造物を享受する眼差しが、その虚軸的性質をうまく使って、再び、創造物の基盤の中へと回り込むという存在の円環性。この円環性が垣間見えたときに、世界が内在の環で繋がれるいることの直観が生まれてくる。精神と物質は物質の根源で繋がっているのだ。そして、その繋がりの覚知から世界の修復が開始されることになる。
こう考えると、その瞬間、瞬間で世界が枝分かれしていくというエヴァレットなんかが提唱している平行宇宙の考え方がいかに馬鹿げたものであるかが分かるだろう。こうした宇宙観は物質のみを実在と考え、見るものとしての内在性を忘却した思考が生み出した完全なフィクションである。信じてはいけない。それこそ宇宙がバラバラに崩壊していくことになる。
By kohsen • 01_ヌーソロジー • 0 • Tags: キュビスム, サルトル, 光子, 想像力, 波動関数