●プラトン座標について………次元観察子ψ1~ψ8の骨格構造
これで次元観察子ψ1~ψ8までの描像についての解説は一応、終わります。今まで書いてきた内容がヌーソロジーでいう「トランスフォーマー型ゲシュタルト」の基礎的な知覚様式です。このゲシュタルト作りはヌーソロジーを単なる構造論に終始させないための重要な作業になります。「観察」子と名がついているように、今までご紹介してきた空間構造は人間の意識に内在と外在という二つの観念を付与するために用意された場の構造と言ってよいものです。ですから、これらの構造を単に図式的に理解してもあまり有意味なものとはなりません。というのも、「わたし」自身がこの構造そのものへと変身しなければ「観察」子にはなり得ないからです。慣れない描像に最初はかなり戸惑われるかもしれません。しかし、今までのテキストを参考にしながら根気強くトレースしていけば、ヌーソロジーが描く新しい世界観、人間観のエントランスが必ず見えてくることでしょう。
さて、これら4つの「たま」のトポロジカルな規則性についても少しだけ触れておきます。現在、ヌースソロジーではこの規則性を「プラトン座標」と名付けていますが、これは次元観察子ψ1~ψ2、ψ3〜ψ4、ψ5〜ψ6、ψ7〜ψ8が作る4つの球空間の階層性が5つのプラトン立体(正四面体・正六面体・正八面体・正12面体・正20面体)の中の正六面体と正八面体が作る外接・内接関係に起源を持っているのではないかと考えているからです。プラトン座標とはこれら次元の差異を識別するための本源的な図形群のことをいい、次元観察子を構成するための幾何学的なイデアとも言っていいものです。
まず、第一のたま「点球」としての球空間Aに内接する正八面体aを作ります。この正八面体における立体対角線(赤色で示した部分)が僕らがモノを3次元と見るときのx、y、z軸に当たります(下図1参照)。
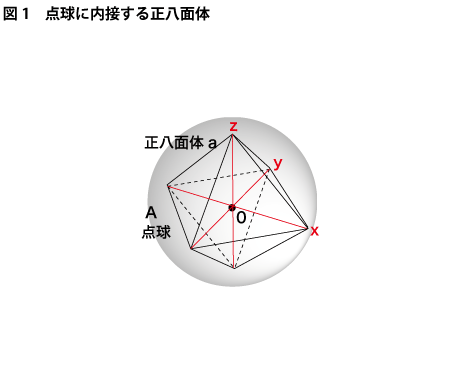
次にこの「点球」に外接する正六面体bとこのbに外接する球空間Bを作ります(下図2参照)。
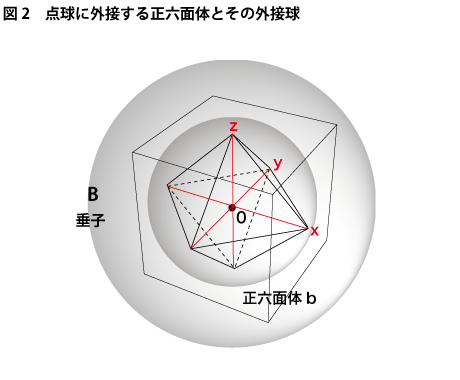
「正六面体bは正八面体aに外接する」という条件から、球空間Aをどんなに拡大しようとも球空間Bには決して到達できないことが分ります。この到達し得ない球空間B上の一点を球空間Aにとっての無限遠点として定義します。このときの球空間Bが次元観察子ψ3~ψ4としての「垂子」となります。
観察子において点球次元と垂子次元の間にどのような差異が出てくるかというと、点球を覆っている球面が垂子次元においては点に変換されてしまうということです。これが今までの解説で何度か顔を出した「面点変換」の概念です。実際の認識において、この面点変換がどのように働いているかを調べてみましょう。
まず、目の前にモノを起きます。そこにはモノの前姿、すなわち表相が見えています。表相はモノをある特定の角度から見た見え姿のことですから、これは点球の中心点Oと点球を覆う球面上の一点を結ぶ半径によって指定されているのが分ります。ここで表相方向をz方向とし、モノをグルグルと回転させてみましょう。モノの隠れていた部分が次々と表相に送り出されてきて、結果的にモノの全表相は点球におけるx、y、zの3軸のうち、x、yの2軸の回転があれば観測者はモノが持つすべての表相をその視線でなめることができます(下図3参照)。
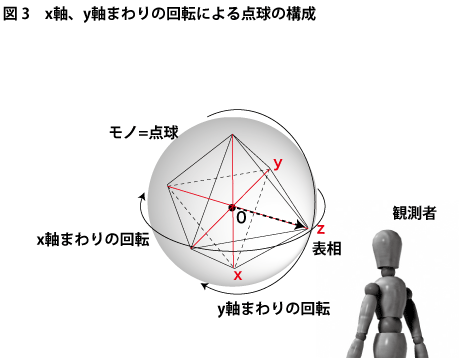
残る3軸目の回転であるz軸まわりの回転は、単純に考えればモノの輪郭を縁取る方向の回転、つまりモノが決して背面側を見せないような回転を観測者に与えてきますが、すでにx、yの2軸の回転の中にこのz方向は含まれていますから、この第三軸回であるz軸まわりの回転はz軸まわりの回転というよりも、x、y、z軸をすべて等化するような回転となっていると考えられます。ここは少し分りにくいでしょうから、図を使って丁寧に説明してみます。
通常、第三軸目に当たるz軸まわりの回転は今いったように、観測者の方向に直立した方向を軸とする回転に見なされがちです。しかし、図3からも分るように、x軸とy軸、2軸の回転によってすでに点球の内部には3次元性の空間が出来上がっています。というのも、x軸の回転で半径部分は円板を作り、今度はy軸の回転でその円板を回転させ、球体自体が出来上がってしまうからです。この時点で球体の内部にはすでにx、y、z方向を含んでいるわけですから、第三軸であるz軸まわりの回転とは実はx、y、z方向を全く別の方向に取りまとめる回転となっているのではないかと考えられます。このことは下図4に示すように、球空間内部のx、y、z方向を観察者から見て「水」の字形に見えるような配置に置くと分りやすくなります。
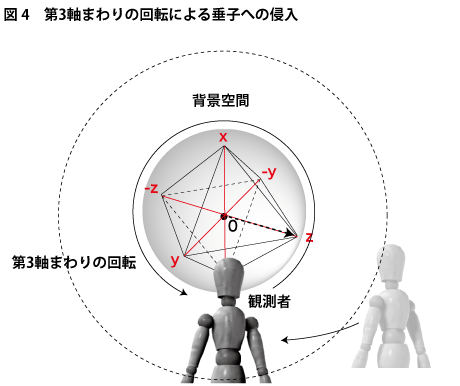
観測者がこの位置から点球の回転を見ると、(x、y、z)と(-x、-y、-z)が回転によって入れ替わるのが分ります。ヌーソロジーでは、この入れ替わりを右手系と左手系の対称性が作り出されている回転と解釈します。つまり、点球の3次元性を射影平面として見なせる方向があると考えるわけです。この回転によって(x、y、z)と(-x、-y、-z)が入れ替え可能になるということは、点球が作る球空間自体の相互反転性の等化になっているということ同意です。このことは、第三軸の回転が4次元性に方向を作り出す負荷のような働きをしているということになります。この方向はちょうど物体の角運動量ベクトルのような形で点球の球面を貫き、次の垂子を覆う球面上の一点へと出てきます。ここはモノを回しても回しても微動だにしない場所、点球の球空間にとっては無限遠点とも呼んでいいような場所、つまり観測者の位置になります。人間の外面においてはそこはモノの背景面のことであり、人間の内面側ではそれは視点と呼ばれているものになります。ヌース(旋回的知性)のψ3への侵入とその反映です。
もちろん、これらの話はすべてヌーソロジーの仮説です。第三軸の回転によって4次元性と連結を持つというところは、数学的に言えばSO(3)を綜合したものが4次元の線分となるということを意味しますが、このことが実際に数学的に証明できるかどうかはよく分りません。しかし、モノと視線の間にはモノをそのまま反転させて見せるようなトリックが仕掛けてあるのは、ネッカーの立方体などでよく知られていることです(下図5参照)。

人間の視覚にどうしてこのような錯覚が起こるのかその原因はよく分っていないと言われていますが、これはヌーソロジーの観点から言えば、垂子における人間の内面と外面の分岐が反映されているものと解釈されます。
以下、ψ3~ψ4、ψ5~ψ6、ψ7~ψ8のへの拡張もすべて同じ法則性で構造化されていきますので、皆さんも、この三つの次元観察子の階層にわたっての実地検証にトライしてみるといいでしょう。観察子構成のためのいいトレーニングになると思います。参考までにその全体像を図示しておきましょう(下図6)。
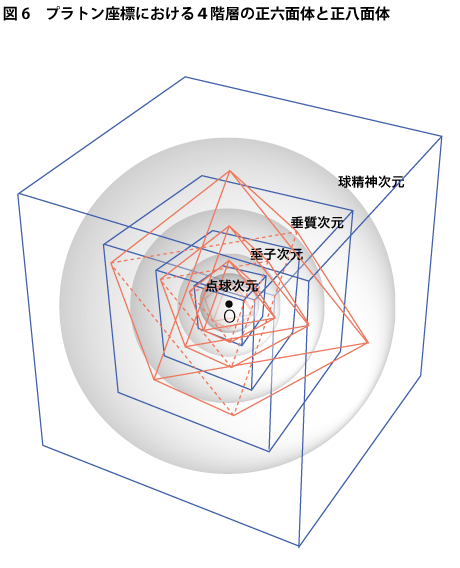
何とも壮観な図です。この図から、人間の意識に表相として出現してきたヌースがスピンを多重化させていきながら、次々と次元を上昇させていく様子が想像できます。この4重の正六面体・正八面体の内接・外接構造が作り出す次元発展のトポロジカルな規則性ヌーソロジーが「プラトン座標」と呼ぶものです。ヌース(旋回的知性)の上昇の仕方がいかに単純なものであるかが分かるでしょう。点球を3軸回転させ垂子の半径に接続し、今度はその垂子の半径を3軸回転させ垂質の半径を作り、次に垂質の半径を3軸回転させて球精神の半径(スピノール)へと至る。最後はこの球精神の半径を3軸回転させて……という3軸回転の四重機構を持ってヌース(旋回的知性)は活動しているのです。皆さんも、皆さんの意識の中に内在しているこのヌースの上昇ルートを是非、追いかけてみて下さい。
――つづく







12月 1 2008
時間と別れるための50の方法(55)
●プラトン座標について………次元観察子ψ1~ψ8の骨格構造
これで次元観察子ψ1~ψ8までの描像についての解説は一応、終わります。今まで書いてきた内容がヌーソロジーでいう「トランスフォーマー型ゲシュタルト」の基礎的な知覚様式です。このゲシュタルト作りはヌーソロジーを単なる構造論に終始させないための重要な作業になります。「観察」子と名がついているように、今までご紹介してきた空間構造は人間の意識に内在と外在という二つの観念を付与するために用意された場の構造と言ってよいものです。ですから、これらの構造を単に図式的に理解してもあまり有意味なものとはなりません。というのも、「わたし」自身がこの構造そのものへと変身しなければ「観察」子にはなり得ないからです。慣れない描像に最初はかなり戸惑われるかもしれません。しかし、今までのテキストを参考にしながら根気強くトレースしていけば、ヌーソロジーが描く新しい世界観、人間観のエントランスが必ず見えてくることでしょう。
さて、これら4つの「たま」のトポロジカルな規則性についても少しだけ触れておきます。現在、ヌースソロジーではこの規則性を「プラトン座標」と名付けていますが、これは次元観察子ψ1~ψ2、ψ3〜ψ4、ψ5〜ψ6、ψ7〜ψ8が作る4つの球空間の階層性が5つのプラトン立体(正四面体・正六面体・正八面体・正12面体・正20面体)の中の正六面体と正八面体が作る外接・内接関係に起源を持っているのではないかと考えているからです。プラトン座標とはこれら次元の差異を識別するための本源的な図形群のことをいい、次元観察子を構成するための幾何学的なイデアとも言っていいものです。



まず、第一のたま「点球」としての球空間Aに内接する正八面体aを作ります。この正八面体における立体対角線(赤色で示した部分)が僕らがモノを3次元と見るときのx、y、z軸に当たります(下図1参照)。
次にこの「点球」に外接する正六面体bとこのbに外接する球空間Bを作ります(下図2参照)。
「正六面体bは正八面体aに外接する」という条件から、球空間Aをどんなに拡大しようとも球空間Bには決して到達できないことが分ります。この到達し得ない球空間B上の一点を球空間Aにとっての無限遠点として定義します。このときの球空間Bが次元観察子ψ3~ψ4としての「垂子」となります。
観察子において点球次元と垂子次元の間にどのような差異が出てくるかというと、点球を覆っている球面が垂子次元においては点に変換されてしまうということです。これが今までの解説で何度か顔を出した「面点変換」の概念です。実際の認識において、この面点変換がどのように働いているかを調べてみましょう。
まず、目の前にモノを起きます。そこにはモノの前姿、すなわち表相が見えています。表相はモノをある特定の角度から見た見え姿のことですから、これは点球の中心点Oと点球を覆う球面上の一点を結ぶ半径によって指定されているのが分ります。ここで表相方向をz方向とし、モノをグルグルと回転させてみましょう。モノの隠れていた部分が次々と表相に送り出されてきて、結果的にモノの全表相は点球におけるx、y、zの3軸のうち、x、yの2軸の回転があれば観測者はモノが持つすべての表相をその視線でなめることができます(下図3参照)。
残る3軸目の回転であるz軸まわりの回転は、単純に考えればモノの輪郭を縁取る方向の回転、つまりモノが決して背面側を見せないような回転を観測者に与えてきますが、すでにx、yの2軸の回転の中にこのz方向は含まれていますから、この第三軸回であるz軸まわりの回転はz軸まわりの回転というよりも、x、y、z軸をすべて等化するような回転となっていると考えられます。ここは少し分りにくいでしょうから、図を使って丁寧に説明してみます。
通常、第三軸目に当たるz軸まわりの回転は今いったように、観測者の方向に直立した方向を軸とする回転に見なされがちです。しかし、図3からも分るように、x軸とy軸、2軸の回転によってすでに点球の内部には3次元性の空間が出来上がっています。というのも、x軸の回転で半径部分は円板を作り、今度はy軸の回転でその円板を回転させ、球体自体が出来上がってしまうからです。この時点で球体の内部にはすでにx、y、z方向を含んでいるわけですから、第三軸であるz軸まわりの回転とは実はx、y、z方向を全く別の方向に取りまとめる回転となっているのではないかと考えられます。このことは下図4に示すように、球空間内部のx、y、z方向を観察者から見て「水」の字形に見えるような配置に置くと分りやすくなります。



観測者がこの位置から点球の回転を見ると、(x、y、z)と(-x、-y、-z)が回転によって入れ替わるのが分ります。ヌーソロジーでは、この入れ替わりを右手系と左手系の対称性が作り出されている回転と解釈します。つまり、点球の3次元性を射影平面として見なせる方向があると考えるわけです。この回転によって(x、y、z)と(-x、-y、-z)が入れ替え可能になるということは、点球が作る球空間自体の相互反転性の等化になっているということ同意です。このことは、第三軸の回転が4次元性に方向を作り出す負荷のような働きをしているということになります。この方向はちょうど物体の角運動量ベクトルのような形で点球の球面を貫き、次の垂子を覆う球面上の一点へと出てきます。ここはモノを回しても回しても微動だにしない場所、点球の球空間にとっては無限遠点とも呼んでいいような場所、つまり観測者の位置になります。人間の外面においてはそこはモノの背景面のことであり、人間の内面側ではそれは視点と呼ばれているものになります。ヌース(旋回的知性)のψ3への侵入とその反映です。
もちろん、これらの話はすべてヌーソロジーの仮説です。第三軸の回転によって4次元性と連結を持つというところは、数学的に言えばSO(3)を綜合したものが4次元の線分となるということを意味しますが、このことが実際に数学的に証明できるかどうかはよく分りません。しかし、モノと視線の間にはモノをそのまま反転させて見せるようなトリックが仕掛けてあるのは、ネッカーの立方体などでよく知られていることです(下図5参照)。
人間の視覚にどうしてこのような錯覚が起こるのかその原因はよく分っていないと言われていますが、これはヌーソロジーの観点から言えば、垂子における人間の内面と外面の分岐が反映されているものと解釈されます。
以下、ψ3~ψ4、ψ5~ψ6、ψ7~ψ8のへの拡張もすべて同じ法則性で構造化されていきますので、皆さんも、この三つの次元観察子の階層にわたっての実地検証にトライしてみるといいでしょう。観察子構成のためのいいトレーニングになると思います。参考までにその全体像を図示しておきましょう(下図6)。
何とも壮観な図です。この図から、人間の意識に表相として出現してきたヌースがスピンを多重化させていきながら、次々と次元を上昇させていく様子が想像できます。この4重の正六面体・正八面体の内接・外接構造が作り出す次元発展のトポロジカルな規則性ヌーソロジーが「プラトン座標」と呼ぶものです。ヌース(旋回的知性)の上昇の仕方がいかに単純なものであるかが分かるでしょう。点球を3軸回転させ垂子の半径に接続し、今度はその垂子の半径を3軸回転させ垂質の半径を作り、次に垂質の半径を3軸回転させて球精神の半径(スピノール)へと至る。最後はこの球精神の半径を3軸回転させて……という3軸回転の四重機構を持ってヌース(旋回的知性)は活動しているのです。皆さんも、皆さんの意識の中に内在しているこのヌースの上昇ルートを是非、追いかけてみて下さい。
――つづく
By kohsen • 時間と別れるための50の方法 • 0 • Tags: トランスフォーマー型ゲシュタルト, プラトン立体, 内面と外面, 無限遠, 表相