時間と別れるための50の方法（48）

　●双子のスピノール
　（47）からの続き→
　さて、もう一度スピノールの描像を順序立てて整理しておきましょう。

1、知覚球体は「わたし」の身体を中心とする3軸回転のうちの2軸での回転によって構成されている。
2、この回転によって構成される知覚球面を「面点変換」という概念操作によって「点」と見なし、知覚球体そのものを4次元方向の線分として解釈する。
3、このとき、この線分は観測者自身の絶対的「前」という方向を意味することになる。
4、絶対的「前」は奥行き方向の一点同一視によって潰されているので、知覚球体は4次元方向の微小長さを持つ一本の線分によって束ねられていると考えられる。
5、この線分を軸とする回転は絶対的「前」であるところの知覚正面そのものの回転となる。
6、このときの回転軸に当たるものがスピノールだと考えられる。
7、よってスピノールは次元観察子ψ5と等価なものと考えられる。

　この描像に沿ってスビノールと通常の空間認識の関係を描写すると下図1のような関係になります。
　

　
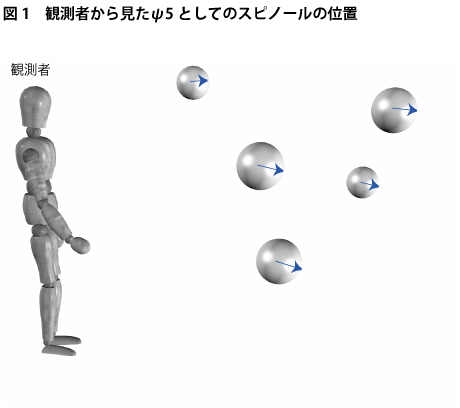
　図を用いた説明では、どうしても客観的な図式になってしまうので少し分かりにくいかもしれませんが、この図に上の説明の描像を当てはめると、観測者にとって奥行き方向はつねに一点で同一視されているので、スピノールは観測者が時空上に観察するあらゆる点状の球体の半径部分にこの図に示したようなかたちで入り込んでくることになります。
　図1では点状の球体を故意に大きな球体として描いています。これは次元観察子ψ1～ψ2の説明にあったように、ヌーソロジーでは点概念とモノ概念（球体概念）を「点球」というヌーソロジー特有の概念で一括りにし、同じものとして考えるからです。点と球体が同じものと聞くと、皆さんは怪訝に思うかもしれません。一般的には点はゼロ次元で球体は3次元とされているからです。しかし、4次元空間の世界はもはや時間が存在していない永遠の場所なわけですから、そこでの対象は実際のモノのかたちというよりもむしろ「観念のカタチ」だと考えられます。

　観念のカタチとは、真の形相とも言っていいものです。たとえば現象世界には完全な円というものは存在しません。しかし、人間の意識はそれを観念として感じ取ることができています。球体の場合は3次元という性格上、その形を知覚に出現させるのは不可能です。「このボールは球体である」と思ったとしても実際に球体という形は目には見えませんし、手で触ったとしても球体という視像が視覚に出現してくるわけではありません。純粋なカタチの世界はプラトンが言うように、観念世界の彼方にその起源も不明なままただ存在しています。こうした「観念のカタチ」という意味においては、点も球体もさほど違いがありません。実際、僕らが3次元空間上に点を打つためには、そこに小さな丸い仁丹のような粒を措定する以外方法はありません。その意味で言えば、むしろ、幅も厚みも高さも持たず、ただ位置だけを持つ、といった従来のユークリッド的な点概念の方が不完全で曖昧な概念なのです。
　ヌーソロジーでは以上のような理由からモノとしての球体の内部を3次元空間の範疇とは見なしません。3次元空間というのはあくまでもモノの外部に広がる空間に対応します。こうした区別を持ち込むのはモノの内部と外部の間に絶対的な差異（次元的な差異）が存在していると考えるからですが、これは物理学的に言えば、今のところスカラー空間かベクトル空間かの違いに対応しているのではないかと考えています。

　ヌーソロジーが考える3次元（ベクトル）空間とはあくまでもモノの外部、モノからその外側に広がっているように感覚化されている空間のことです（この領域は以前説明したように観察子でいうとψ3～ψ4に当たります）。このことは観測者（モノの背景面）の存在があってこそ初めて空間に方向が与えられるということを意味しています。空間に方向を与えている力の本質とは観測者の意識の存在だということです。このへんは説明が長引くので、また、別の機会に詳しく説明していきましょう。
　さて、話をスピノールに戻します。ここでモノを挟んで「わたし」と対峙し合う「あなた」という別の主体の存在を想定してみることにします。すると、「あなた」を取り巻いている知覚球体もおそらく「わたし」の知覚球体が一つのスピノールφによってまとめられたように、原点Ｏを挟んで逆方向を向いたスピノールφ*として活動していることが予想されます（下図2参照）。
　

　
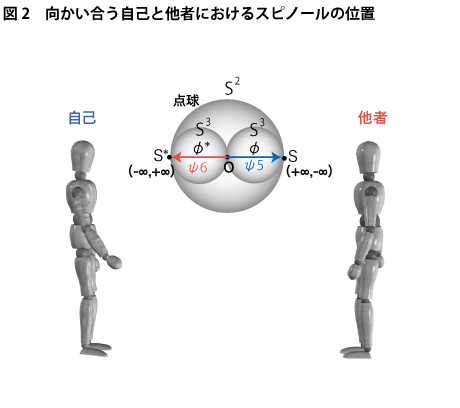
　このスピノールφ*は「わたし」側からしてみれば、わたしが「前」を見ているときに常にその前を背後で支えている「後」の集合、つまり観測者にとっての絶対的「後」に当たるものですから、今までの話の流れからすればこれは次元観察子ψ5の反映としてのψ6に相当してきます。当然。「あなた」側から見れば、これらψ5とψ6の関係はψ*6とψ*5の関係になっており、この二つのスピノールは言うまでもなくキアスム（交差配列）の関係を形作っています。つまり、「あなた」と「わたし」の関係においては、等化作用と中和作用の関係が正反対になっていて、どちらも3次元における無限遠点にその主体本来の位置を持ってはいるのですが、それぞれの位置はS（＋∞、－∞）とS*（－∞、＋∞）として互いに表裏を逆にした関係を形作っているわけです。

　このSとS*の位置関係は、4次元空間においては原点Ｏを挟んで対称的な位置関係を持っていますが、3次元空間では区別する術がありません。以前に挙げたメビウスの帯で喩えれば、ちょうど一周して辿り着くウラの世界だと思って下さい。3次元空間の球面上にはこのような捻れが存在していないので、SとS*はリング上の同じ位置にしか見えないわけです。このような捻れを実際の空間認識でどのように描像すればいいかというと、おおよそ次のようなイメージになると思われます。

　たとえば、皆さんは、普段、モノが目の前にあるとき、その手前に自分がいると考えているはずです。そして、その位置はモノの位置を原点Ｏとすれば、3次元上のある一点として表せると思っていることでしょう。もちろん、それは3次元認識の範疇では間違いではありません。しかし、そうやって指定された「わたし」の位置は、客観的に外部から自分を見たときの物質的肉体としてのわたしの位置であって、今までお話してきたように持続を持った実際の観察の現場としての「わたし」の位置ではありません。
　この「持続を持った観察の現場としてのわたし」の位置を指定する空間が4次元だと考えて下さい。その位置は3次元認識では肉体の位置のように感覚化されていますが、本来は4次元方向に位置しているので、3次元空間上では無限遠点Sとしか言いようのない場所になり、それはまた光速度の世界であるがゆえに無限小の長さの中に入り込んできます。そして、モノを挟んでそこで向かい合って対峙している「持続を持った観察の現場としてのあなた」も当然のことながら4次元空間上の位置S*を持って無限小の領域の中で対峙していることでしょう。

　4次元空間で対峙するこうしたスピノールを次元観察子ψ5とψ6に対応させると、スピノールの回転はこれら両者を等化している運動ではないのかという推測が立ってきます。ψ5とψ6の等化はヌーソロジーでは次元観察子ψ7の領域への意識の侵入を意味しますが、これは自己の意識場と他者の意識場を入れ替えても何の影響も受けない、つまり、自他間の変換対称性を持つ空間の生成運動の次元になってきます。平たい言い方をすれば、スピノールが回転している次元は「わたし」と「あなた」の区別がなくなった空間を作り出しているわけです。次回はその詳細について書いてみます――つづく