時間と別れるための50の方法（45）

●メビウスの帯とスピノール………（1）
　さて、スピノールの話を続けます。ここからの話をより分りやすくするために、前回の図2における正六面体の内接球だけを引っこ抜いて、ここに図1として示します。この球空間がスピノールが活動している空間になります。

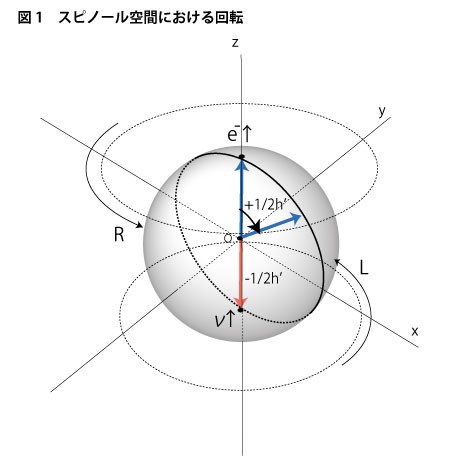
　この図で±1/2h’の長さで表されている矢印が数学的にはスピノールに対応します。このスピノールは+1/2h’がアップスピンと呼ばれ、-1/2h’がダウンスピンと呼ばれるものになりますが、図に示した回転Rの方向によって（つまり、角運動量の方向に対して右回転か左回転かによって）、極性が反転します。こうした組み合わせが、たとえばレプトンであれは、電子とニュートリノのアップスビンとダウンスピンの対を作ってきます（実際に観測にかかるのは左巻きのニュートリノだけとされていますが、これはヌーソロジー的には右巻きのニュートリノが観測の場そのものとしての時空として化けているからではないか、ということになります）。ここではあとの説明で出てくる次元観察子ψ5とψ6との絡みからダウンスピン側を左巻き（L）のニュートリノのスピンとして考えることにします。
　両スピンとも単なる矢印で表されているので、一見普通のベクトルと何ら変わらないもののように見えてしまいますが、ここに表されたスピノールはベクトルとは全く違った性質を持っています。否、ベクトルとは全く違った性質を持っているからわざわざ「スピノール」という名称が与えられていると思った方がいいでしょう。

　では、普通のベクトルとスピノールはどう違うというのでしょうか。今、原点Ｏを中心として電子e-↑の方をx-z平面で回転させてみることにしましょう（図1参照）。これが普通のベクトルであれば360度回転させれば元のところに戻ってくるはずです。しかし、スピノールはそうはいきません。数学的に定義されている性質から360度回転させてもなぜかダウンスピンの場所（赤い矢印の部分）にしかたどり着けないのです。そして、スピノールが回転によって元のところに戻ってくるためには720度、つまり普通の回転で言えば2回転しなければならないとされます。つまり、スピノールが張られてるこの3次元の球空間は一回転が720度に相当するような性質を持っているわけです。実際の3次元空間ではこのようなことは起こり得ませんから、この球空間は物理学では「内部空間」と呼ばれ、時空上の一点一点に貼付けられた数学的な抽象空間の扱いを受けます。

　要は、この内部空間においては、180度に見えている角度は実際の3次元空間上では360度に対応しており、アップスピンを360度回転させるとダウンスピンに変わり、もう360度回転させることによって、ようやく、元のアップスピンに戻るということなのです。よく、一般向けの解説書を見るとスピノールは720度回転で対称性を取り戻す、と書いてありますが、その内容はこうした意味を指して言っているわけです。。。う〜ん、分らない。。という皆さんのうめき声が聞こえてきそうです。はてはて、一体このスピノールとは何物なのでしょうか？

　720度回転して元の位置に戻ってくる——スピノールが持っているこうした奇異な性質の喩えはよく「メビウスの帯」で説明されます（下図2参照）。今、図2に示したように、メビウスの帯上をアリが歩いている様子を想像してみて下さい。この帯の上をアリが一回転してくるとちょうどスタート地点の真裏に来るのが分ります。そして、このアリはもう一回りしてようやく元のスタート地点に戻ってくることができます。スピノールの回転も単純な回転ではなく、このメビウスの帯のように回転軌道が進行方向に沿って捻られているような形になっているために360度回転しただけでは元の位置には戻らず、720度回転して初めて元の位置に戻るような性格を持っているわけです。

　さて、ここで、ヌーソロジーの話に戻りましょう。無限小の長さにまで潰された観測者の絶対的前を回転させている4次元軸、これが次元観察子ψ5の位置であり、これこそが物理学のいうスピノールの正体になっているのではないか、と前回の記事で強調して書きました。このような考え方がスピノールが持つこの「720度回転して対称性を取り戻す」という特性とうまく合致すれば、とりあえずは、次元観察子ψ5=スピノールという推測がそれほど的外れな主張ではないということが言えるはずです。
　では、さっそく検証に入りましょう。まずは、以前ご紹介した次元観察子ψ5〜ψ6の図を再度、引っ張ってきてみることにします（下図3）。

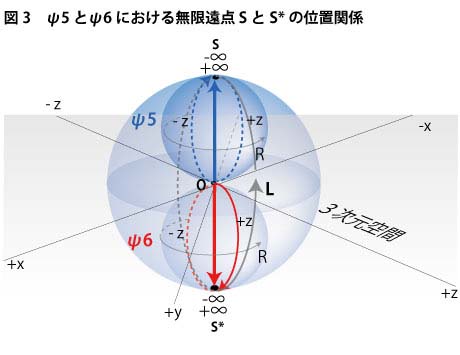
　元々、次元観察子ψ5の位置を決定していた場所がどのような性格を持っていたかと言うと、ここは相互反転した3次元の球空間の＋∞と−∞に当たる場所でした。つまり、次元観察子ψ5を示す矢印の先端の位置は3次元空間上の位置のように単純に一点で指定される場所ではなく、S=（＋∞、−∞）というように相互反転した3次元空間における二つの無限遠点の重合によって指定されている場所になっていたわけです。
　反対向きの矢印についてはどうでしょうか。こちらは中和側=次元観察子ψ6です。この中和側は人間の内面の意識側から見れば今まで説明してきたように時空、つまり無限の広がりを持つ3次元双曲面の自転軸に当たりますが、等化側であるψ5から見れば、自分自身の反映なわけですから、当然、こちらも無限小の長さを持つ4次元方向の回転軸に見えているはずです。そして、このψ6の矢印の先端の位置は次元観察子ψ5側とは外面と内面の関係が逆になっているわけですから今度はS*=（−∞、＋∞）によって指定されています。つまり、ψ5とψ6を規定する重合した無限遠点の位置は4次元から見ると、射影空間的な性質を持っており、表裏が逆の関係にあるわけです。
　ここで、次元観察子ψ5が電子のアップスピン、ψ6がニュートリノのアップスピンとしてのスピノールを意味しているとすると（ψ6の回転Rを逆方向に取ればψ*5となって電子のダウンスピンとも考えることができます）、物理学でいうスピノールの回転とは、ヌーソロジー的にはこれら次元観察子ψ5とψ6を等化するための回転Lとして解釈することができます（ψ7の方向性を作り出しているということ）。ψ5とψ6はともに4次元方向において正反対を向いている矢印ですから、両者を等化するためのこの回転は当然のことながら4次元空間上での回転となります。図からも分るように、この4次元空間内で半回転させれば、S（＋∞、−∞）とS*（－∞、＋∞）が入れ替わることができるわけですが、このとき、Sの（＋∞、－∞）とS*の（－∞、＋∞）の関係を裏返すような回転の位相が、この4次元の回転には隠されているわけです。この4次元回転の軌道Lに沿ってもう半回転させれば、ψ5は元のψ5の位置としての（＋∞、－∞）に戻ってくることができます。
　さて、さて、次元観察子ψ5とψ6も半回転すると（＋∞、−∞）と（−∞、＋∞）が入れ替わるような構造を持っていることが分ってきました——このこととスピノールとはどのような関係にあるのでしょうか。例のメビウスの帯を使って、次のような考え方を作れば両者の関係をうまく説明することができます。
——つづく