10月 16 2008

時間と別れるための50の方法（44）

●スピノール登場
　（前回のつづき）この接続を達成するためには、やはり、そのときの空間の構造が重要なカギを握っているのではないかと思います。位置の等化=次元観察子ψ5の幾何学的構造とは時空上のあらゆる点に貼り付つけることができる超ミクロの3次元球面とその自転軸のことだったことを思い出して下さい。もし、こうした空間構造を持つ何ものかが科学者たちにとっての実存として実際に目の前の時空に存在しているのならば、それこそヌーソロジーが描像している自己という存在の場所性が多くの人に合意形成を得ている従来の科学体系と確固とした連結を伴ってこの現実世界に接続してくることになります。つまり、宗教のような超越的な言説、哲学のような観念的な言説を持ち込まずとも、人間存在に対する見方を今までの人間の現実の中から全く別のものへと変革させていける可能性が出てくるわけです。

　時空上のあらゆる点に貼り付いた超ミクロの大きさの3次元球面とその自転軸――ヌーソロジーの考え方からすれば、これが「わたし」自身の正体でもあるわけですが、この4次元方向を向いた回転軸はおそらく物理学者たちがスピノールと呼んでいるものではないかと考えられます。これははっきり言ってとても非常識な内容です。ですから、それだけに強度もあるので、再度、強度を強調してリフレインしておきます。――奥行きの同一視によって長さ無限小にまで縮められた4次元軸としての観測者の絶対的前方向、これが物理学者たちがスピノールと呼んでいるものの正体だと考えられます。

　もしこの予想が正当性を持つことになれば、僕らは物質と精神の結節点らしきものを初めて描像することに成功したことになるでしょう。というのも、スピノールとは物理学では物質を作る元となっている電子やクォークの自転角運動量（スピン）として登場してくるからです。つまり、人間の外面としての働きである持続-記憶や未来に対する直感はひょっとすると電子やクォークそのものの中にそのすべてが蓄えられているのかもしれない、ということです。
　ということで、スピノールそのものの話に入る前に、電子の自転角運動量という概念について物理学がどう語っているか簡単にダイジェストしてみます。自転角運動量といってもよく分からない人もいるでしょうから、まずは通常の物体の角運動量について簡単に説明しておきましょう。

　角運動量とは回転している物体が持っている運動量のことを言います。通常の運動量pは質量mと速度vの積mvで表されますが、角運動量の場合はこの運動量pに回転している円の半径rを掛け合わせ、

L=p×r（ベクトルの積です）
角運動量 : L　 運動量 : p=mv　回転半径 : r

として表されます。角運動量はベクトル量なので当然、方向を持ち、この方向は回転面に対して垂直な方向、つまり回転軸の方向に現れます。例えば車輪が回っているとするとその車軸の方向ですね。通常の物体の回転はモノが回っているわけですから、その回転は群でいうと2次元回転群SO(2)です。このとき、軸は回転面x-yに対して垂直なz方向に立ち上がり、その方向に自転角運動量ベクトルを形作ってくるわけです（下図1参照）。
　
44_1
　
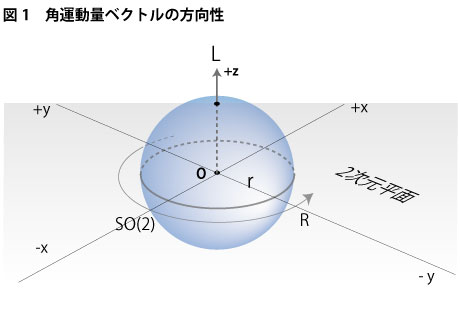
　これは「回転とは等化の本質である」というヌーソロジーの論理を使えば、回転という運動にによってx軸とy軸が等化され（対称性を持ち）、2次元から3次元方向にz軸という方向性を作った、という言い方ができます。レベルは低いですが一種のアセンション（次元上昇）です。回転運動が持っているこのような次元上昇の仕組みをまずはここでしっかりと頭に入れておいていただければと思います。というのも、ヌーソロジーが説くヌース（旋回的知性）とは、回転（等化）によって認識の視点を次元上昇させていく知性の在り方のことを言うからです。その意味で言えば、通常の自転角運動量とは2次元に対する観察子位置を3次元に作り出すための負荷ということになるのかもしれません。次元観察子で言えば、ψ1～ψ2レベルからψ3～ψ4レベルへの意識の侵入力です。

　まぁ、このへんのヌーソロジー自体の内容は後に回すとして、話を元のスピンに戻しましょう。
　一般に電子やクォークも自転していると考えられています。ここで「一般に」と言ったのは、厳密にはこれらの粒子の自転の場が3次元空間ではなく内部空間と呼ばれている描像不能な場所なので、果たしてそれらの自転を通常の物体の自転のように考えていいかどうかが分らないからです。しかし、回転の性質を持っているといういう意味ではやはり角運動量が存在しています。このときの角運動量がスピン角運動量と呼ばれているものです。スピン角運動量は磁場方向の成分（スピン量子数msと呼ばれます）を取ると常に一定となっており、その値は±1/2h’（h’=h/2π）です（hはプランク定数で光1振動分のエネルギーを表します）。ヌースでもよく話が出てくる「スピン1/2」というのはこの値のことを指しています。
　物理学の言葉が一挙に出てきて、ちょっと話が分かりにくくなったかもしれないので、イメージが涌くようにスピンの詳細を図で説明しておきます。
　
44_2
　
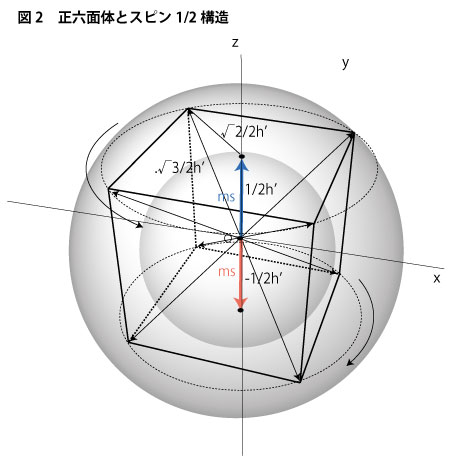
　電子やクォークが自転していると言っても、その自転軸はピンッと直立不動で立っているわけではありません。上図2に示すようにちょうど回転力が衰えたときのコマのように回転軸自体が傾斜して回っています。このとき傾斜軸の角運動量は√3/2h’とされています。そして、このとき起こっている傾斜軸自体の回転におけるz方向の成分がスピン量子数と呼ばれるものです。ピタゴラスの定理からz方向の成分の値がさきほどご紹介したように±1/2h’になっているのが簡単に分ると思います。この比の関係性はちょうど直径√3の長さを持つ球体に正六面体を内接させて、その4本の立体対角線をすべて「等化」させるような回転が起こっていると考えればイメージが簡単になります。つまり、この回転の磁場方向の成分を表すスピン量子数±1/2という値は、この正六面体に内接する球体の半径の大きさに対応してくるわけです。このように、電子やクォークのスピンの成り立ちには1:√2:.√3という正六面体の構成比が深く関係しているわけです。このことは、物質の根底が極めてシンプルな幾何学比によって支配されているということを示唆しています。
――つづく

By • 時間と別れるための50の方法 • 7 • Tags: , , ,