9月 30 2008

時間と別れるための50の方法（39）

●知覚球体と4次元軸
　（38）からのつづき——前回の最後に「知覚球体が次元観察子ψ5」という旨のことを書いてしまいましたが、記憶力のいい方は「あれ？ちょっと前の説明と違うんじゃない」と思われたかもしれません。そうです。第34回の図1における説明では、観測者における3軸回転の綜合（数学の言葉では3次元回転群/S0(3)）を次元観察子ψ5のカタチとしています。しかし、知覚球体を包んでいる知覚球面は（これは2次元球面ですからS^2で表しましょう）は身体の左右方向（これをx軸としましょう）と上下方向（これをy軸としましょう）の2軸による回転によって作り出すことができます。ということは、ψ5としての正確なカタチである観測者のSO(3)を作り出すためにはz軸、つまり前後方向そのものを軸とした回転を加味する必要性が出てきます。この回転は視線回りの回転ですから知覚正面自体の回転の意味を持つことになります。ちょっと実際には作り出しにくいですが、首を傾げるときに生まれている回転の方向のことですね。その意味で、ψ5の正確なカタチは下図1に示すように「知覚球面を知覚したときにおける、そのときどきの視線を軸とした回転の綜合」といえます。
　
401
　
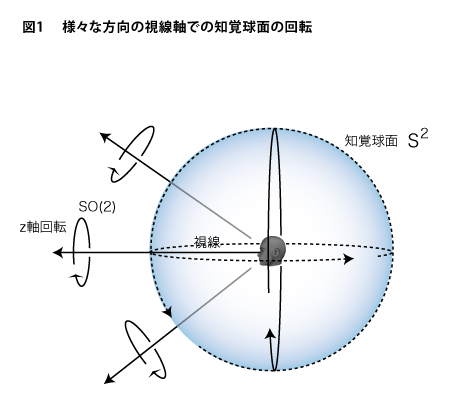
　このカタチの描写はダイレクトには図示できないので、比喩的な言い方になりますが、知覚球面上のあらゆる点に槍が突き刺さって、その一点一点上でグルグルと渦が起こっているような状況です。数学では3次元回転群SO(3)は2次元回転群SO(2)と2次元球面S^2の積として表すことができます。

　SO(3)=S^2×SO(2)

　では、このような観測者自身の回転の綜合は3次元球面S^3に対してどのような運動として現れてくるのでしょうか。以前、次元観察子ψ3～ψ4の説明のところで、視線は4次元方向の線分ではないのかという予測を立てました。あのときは、観測者が一つのモノの周囲を回ったところに綜合化されている球空間の半径部分は、結局、どの半径を取ろうとも「身体の前」であるがゆえに、この「身体の前」を不動な方向と考えて、視線自体を4次元の方向と見なしてよいのではないかと推論しました。

　この次元観察子ψ5のレベルでも全く同じことが起こっているのが分ります。観測者がその場でいくらグルグルと自転しようとも、そこに現れる風景は身体側を基準として見ればやはり「前」という名の一方向にすぎません。僕らはついつい「前」が回っているという表現を取りがちですが、実際には「前」は顔面が向いている方向を指す言葉なわけですから、知覚球面自体も身体を基準とした空間から見れば「面」ではなく、「常に前という一方向に存在する」という意味で「点」と見なす必要が出てきます。つまり、ここでも例の「面点変換」の考え方が生きてくるわけです。そうすると、このとき、知覚球体自体はそれこそ「世界に対する観測者の不動の視線」という意味で、4次元方向に引かれた線分の意味を持つことになります。つまり4次元の方向を描像するためには従来の球体認識を線認識に変える必要があるということです。

　ということは、上に書いた「知覚球面を知覚したときにおける、そのときどきの視線軸に対する回転」とは、結局のところ、4次元方向を軸に持つ回転が3次元認識においてバラバラにされて現れてきた状態ではないのかと考えることができます（あくまでも推理です。数学的な証明は分りません）。前回の解説における図3を用いてこの視線軸に対する回転の綜合の様子を表せば、今度は3次元球面そのものに4次元方向を軸とした回転Eが与えられているイメージが作り出されてきます（下図2参照）。つまり、4次元軸での3次元球面の回転というのは、知覚球面上の様々な方向へ放たれた視線回りの回転を一つの回転に置換する意味を持っているのではないかということです。そして、これはいい換えれば、身体における絶対的前方向を軸とする回転だともいえます。
　
40_2
　
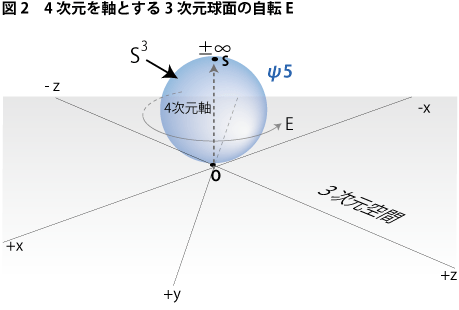
　「わたし」がどのように動こうとも決して動くことのない「前」。車が走行している様子であれ、飛行機が航行している様子であれ、太陽が運行している様子であれ、そして、たとえ「わたし」が歩行している様子であれ、例の眉間鉛筆よろしく、すべての運動はこの視野空間という「不動の前」において認識されるしかないのです。ということは、この「不動の前」とは4次元空間上の3次元球面の自転軸に対応させることが可能になってきます。言い換えれば、この軸は主観が視覚として経験できる全空間を幾何学に綜合したものとなっているわけです。

　次元観察子ψ5。3次元球面とその自転軸。それはヌーソロジーでは自己の場を規定する観察子として定義されます。これは「わたし」が視覚的に触れることのできる全空間のカタチを意味しているということです。そして言うまでもなく、この軸もまた奥行きが一点同一視されていますから、人間の内面認識にとっては長さが無限小にまで縮められた超ミクロの世界に存在していることになります。——つづく

By • 時間と別れるための50の方法 • 4