時間と別れるための50の方法（37）

●3次元空間を丸める
　さて、さて、前回の続きです。自分の周囲に広がる空間の果てのどの方向を見ても、自分の後頭部が見える？？このことは一体何を意味しているのでしょうか。ここはもっと頭をスッキリとさせなければなりません。こういう状況は次元を一つ落として2次元で考えるととても分りやすくなります（下図1参照）。

　
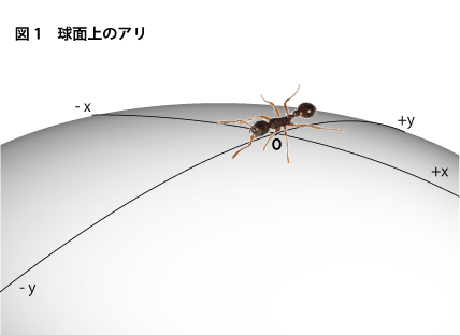
　今、大きな球面上にアリが一匹います。アリにとってはこの球面が無限の平面世界のように見えています。そこにアリ神がやってきてアリに交信を送ります。

　「全きアリよ。おまえの遥か前方を見よ。」
　「ほよよよ。遥か前方………と言われても、視力が追いつきませんがな。」
　「肉の目ではなく、心の目で見るのじゃ。」
　「ほよよよ。。よよ。」
　「心の目で見れば、そこにはおまえの後ろ姿が見えることじゃろう」
　「あっしは複眼なんで、そんなこと言われても………………。」
　「へ理屈はよい。どうじゃ、見えたか。」
　「ほよよよ………はぁ、おぼろげですが。」
　「よろしい、では、そこで、グルリと回ってみなさい。今度は何が見えるかな。」
　「ほよよよ………後ろ姿しか見えない、ということにしておくざんす。。」
　「まぁ、それでよい。わしがおまえに教えたかったことは、”うしろの正面”とは、おまえ自身の顔面だということなのじゃ。このタマの仕組み、よくこころしておくのじゃぞ。」
　「ほよよよ。よぉ分らんですが、アリ神さまのありがたきお言葉として聞いておきますざんす。ほよよよ。」

　次元観察子ψ5のカタチとは、ここでの2次元がそのまま3次元に拡張されたものと考えるといいと思います。つまり、観測者の前方向はx、y、z方向のどちらを向こうとも、どの方向も意識が持った指向性の構造としては実際は無限遠点で円環状に閉じているということです。
　このようにx、y、zの3次元の各方向が円環構造を持った3次元空間は数学では3次元球面と呼ばれ、S^3（エス・スリー）という記号で表されます。通常の球面（2次元球面/S^2という記号で表します）が3次元空間の中で埋め込みが可能となるように、この3次元球面は4次元空間の中で埋め込むことが可能になります。要は4次元球体の表面が3次元球面になっていると考えるわけです。その意味で、3次元球面S^3の直径に当たる部分は当然、4次元の方向になります。
　さて、3次元球面の話は以前、このシリーズの第19回目で行なった次元観察子ψ3の解説でも出てきたと思いますが、ψ3はモノから広がる空間における無限大方向の球面を一点に同一視したところに形作られた3次元球面でした。次元観察子ψ5の場合は、観測者から広がる空間における無限大方向の球面を一点に同一視したときに形作られる3次元球面ということになります。では、この二つの一体何がどう違うのかを調べていくことにしましょう。
　実際の3次元球面を図にするのは不可能なので、『人神/アドバンストエディション』でも使用した図を使って、次元を一つ落とした形で比喩的にアナライズしながら考えていくことにします。

　まず、原点Ｏを持つ3次元空間を平面（x、y、z）で表します（下図2参照）。

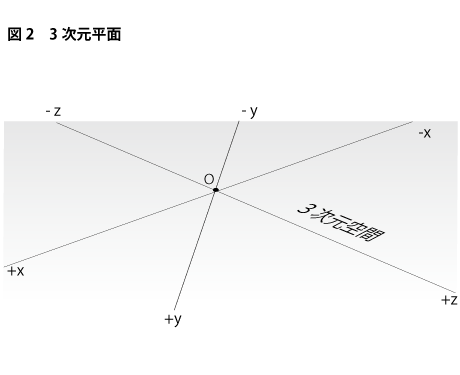
　次に、この平面に垂直な方向を4次元方向と見立て、4次元方向にこの3次元平面を丸め、次元観察子ψ3のカタチを作ります。3次元平面上の無限遠が4次元軸上で無限遠点Sとして一点同一視され、3次元球面状のカタチを作っていることが分ります（下図3参照）。

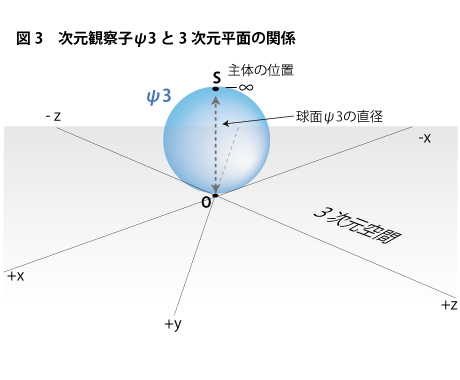
　次に、ここに次元観察子ψ4を付け加えてみます。次元観察子ψ4は以前の解説では3次元双曲面というカタチで表しましたが、ここでは話を分りやすくするためにψ3と同じ3次元球面とし、無限遠点の位置に白い穴を開けて表すことにします。これはψ4側ではモノから広がる空間の無限大方向が一点同一視されておらず、想像的な「後」方向の中で開きっぱなしになっているという意味を持たせています。このことは、ψ4ではψ3のように知覚が存在していないので「知覚=主体」とするための位置が生まれておらず、無限遠点が「主体」という差異の概念で埋められていないということを意味しています。一方のψ3が形作る3次元球面は無限遠点を黒い点で表しています。これは、ここに主体という差異の概念が収まっているという意味です（下図4参照）。

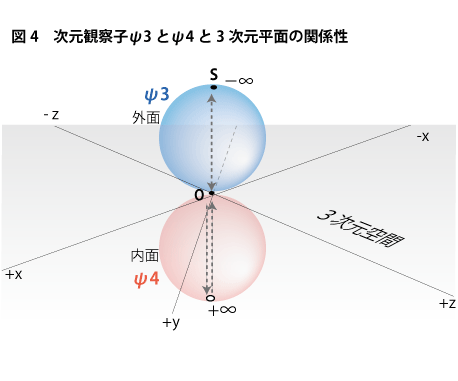
　「次元観察子ψ3=人間の外面、次元観察子ψ4=人間の内面」というヌースの特異な概念が、この4次元から見た図では文字通り「面」として表されているのが分かります。次元観察子ψ3とψ4は3次元平面が互いに4次元の逆方向に丸められているために、それぞれの球面における表裏の関係が逆になっています。つまり、ヌース理論は3次元空間自体を「面」と呼べるような位置、つまり4次元の高みから3次元空間を見て、その表裏を区別するために「人間の内面」や「人間の外面」という言葉を用いているということです。——つづく