●モノから広がる空間と観測者から広がる空間は全く違うもの
さて、これから次元観察子ψ5とψ6の球空間について、その幾何学的な構造を大まかにチェックしていってみたいと思います。前回の図1からも推測できるように、ψ5の球空間の方は現実として見える前方向(光速度状態として奥行きが無限小の長さにまで潰された前方向)が回転によって作り出した球空間、ψ6の球空間の方は想像的「後」方向がその回転によって無限大の広がりを作り出している球空間ということになりますが、幾何学的にこの両者はどのような関係で表すことができるのでしょうか。まずは、NC上でこれら両者のカタチの成り立ちを見てみることにしましょう。
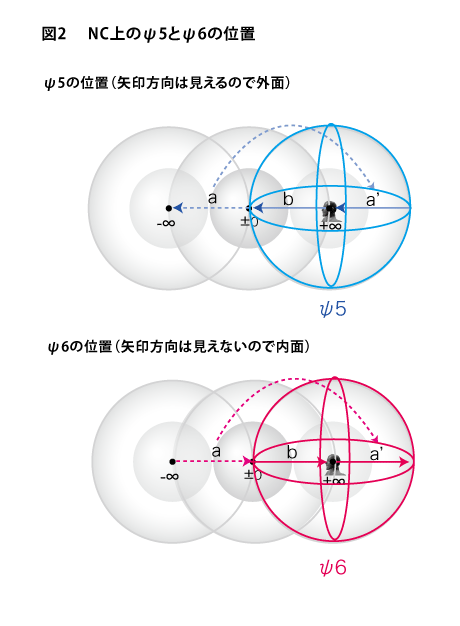
NC上で観測者の前を表すにはいろいろな方法がありますが、最も分りやすいのはモノの背後側(矢印a)とモノの手前側(矢印b)を合わせ持った場所を「観測者の前方向」と見なすことでしょう(下図1)。結果的に、この矢印aと矢印bをつないだ矢印を観測者を中心に3軸で回転させた空間がψ5の球空間ということになりますが、これだとψ3〜ψ4の球空間との区別がつきにくいので、ここでは次のような別の見方を取ることにします。

モノの背後方向を表していた矢印aは、見方を変えれば、観測者の後方に突き刺さってくるような矢印でもあることが分かります。そこで、この矢印aを右側の球体C側の方に移動させて表現し、矢印a’とします。するとψ5の球空間を作るためには矢印bと矢印a’をつないだ矢印、つまり、右側の球体Cの直径幅の矢印をそのまま3軸回転させればいいことが分かります。同様にψ6は人間の内面側なのでψ5の球空間の直径を作っている矢印とは反対方向の矢印を直径として、そのままこの直径を回転させたときにできる球空間と考えるといいでしょう(下図2参照)。
このように、NC上での次元観察子ψ5〜ψ6の球空間の成り立ちを見て言えることは、モノから広がる球空間(次元観察子ψ3〜ψ4)と観測者から広がる球空間(次元観察子ψ5〜ψ6)は、互いに全く次元が違うものだということです。3次元認識に捕われた見方で見てしまうと、モノも観測者も同じ物体にしか見えませんから、それらの回転が作る空間も観察子で言えばψ3〜ψ4レベルの空間となってしまいます。しかし、人間の外面(観測)という概念が考慮されると、観測者から広がる球空間はモノから広がる球空間に比べてその半径が2倍になっていることが分かってきます。NCで言えば、ψ3の球空間の半径は上図に示した点Oと−∞を結ぶ線でしたが、ψ5の半径は+∞と−∞を結ぶ線になっているということです。
この2倍の半径の意味は結果的に、観測者から広がる空間がモノから広がる空間を無数持ち合わせた球空間になるということになって反映してきます。これは実際に確かめてみればすぐに分かります。「わたし」がグルっと回ってどこに視線を向けようが、その視線上の一点には、その一点を中心とするようなモノから広がる空間を想定することができますよね。言い換えれば、次元観察子ψ5〜ψ6という球空間はそれぞれが無数のψ3〜ψ4の集合で構成されているということなのです。
さて、おそらく上でのNC上でのψ5とψ6のイメージは分かりづらかったと思いますので、ここでもう一歩突っ込んで、次元観察子ψ5とψ6の球空間がどのようなカタチを持っているかを調べてみましょう。ψ5の球空間の中心点はNCを見て分るように+∞と−∞の重合点になっています。これは観測者の位置そのものです。この重合のイメージを取りあえず実際の空間上で作ってみることにしましょう。すると、ちょっと奇妙な描像ですが、それはおおよそ次のようなイメージになってきます(下図3参照)。
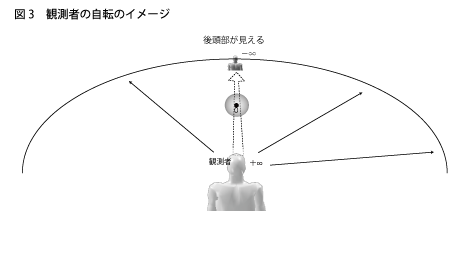
目の前にモノがあります。その背後に遥か彼方まで延びる無限の長さの直線があります。そして、その直線が無限遠点(−∞)に達したところに自分がいます。しかし、そこに見える自分は自分の後頭部です。このことを想定した上でグルっと回ってみましょう。すると、回っても回ってもその視線の彼方にやはり自分の後頭部が見えることになります。つまり、次元観察子ψ5という球空間は観測者が知覚球面を形作ったときには、その球面上のどの方向にも観測者自身の後頭部が見えるような構造になっているということです。はて、はて?何のこっちゃ?——つづく







9月 16 2008
時間と別れるための50の方法(36)
●モノから広がる空間と観測者から広がる空間は全く違うもの
さて、これから次元観察子ψ5とψ6の球空間について、その幾何学的な構造を大まかにチェックしていってみたいと思います。前回の図1からも推測できるように、ψ5の球空間の方は現実として見える前方向(光速度状態として奥行きが無限小の長さにまで潰された前方向)が回転によって作り出した球空間、ψ6の球空間の方は想像的「後」方向がその回転によって無限大の広がりを作り出している球空間ということになりますが、幾何学的にこの両者はどのような関係で表すことができるのでしょうか。まずは、NC上でこれら両者のカタチの成り立ちを見てみることにしましょう。
NC上で観測者の前を表すにはいろいろな方法がありますが、最も分りやすいのはモノの背後側(矢印a)とモノの手前側(矢印b)を合わせ持った場所を「観測者の前方向」と見なすことでしょう(下図1)。結果的に、この矢印aと矢印bをつないだ矢印を観測者を中心に3軸で回転させた空間がψ5の球空間ということになりますが、これだとψ3〜ψ4の球空間との区別がつきにくいので、ここでは次のような別の見方を取ることにします。
モノの背後方向を表していた矢印aは、見方を変えれば、観測者の後方に突き刺さってくるような矢印でもあることが分かります。そこで、この矢印aを右側の球体C側の方に移動させて表現し、矢印a’とします。するとψ5の球空間を作るためには矢印bと矢印a’をつないだ矢印、つまり、右側の球体Cの直径幅の矢印をそのまま3軸回転させればいいことが分かります。同様にψ6は人間の内面側なのでψ5の球空間の直径を作っている矢印とは反対方向の矢印を直径として、そのままこの直径を回転させたときにできる球空間と考えるといいでしょう(下図2参照)。
このように、NC上での次元観察子ψ5〜ψ6の球空間の成り立ちを見て言えることは、モノから広がる球空間(次元観察子ψ3〜ψ4)と観測者から広がる球空間(次元観察子ψ5〜ψ6)は、互いに全く次元が違うものだということです。3次元認識に捕われた見方で見てしまうと、モノも観測者も同じ物体にしか見えませんから、それらの回転が作る空間も観察子で言えばψ3〜ψ4レベルの空間となってしまいます。しかし、人間の外面(観測)という概念が考慮されると、観測者から広がる球空間はモノから広がる球空間に比べてその半径が2倍になっていることが分かってきます。NCで言えば、ψ3の球空間の半径は上図に示した点Oと−∞を結ぶ線でしたが、ψ5の半径は+∞と−∞を結ぶ線になっているということです。
この2倍の半径の意味は結果的に、観測者から広がる空間がモノから広がる空間を無数持ち合わせた球空間になるということになって反映してきます。これは実際に確かめてみればすぐに分かります。「わたし」がグルっと回ってどこに視線を向けようが、その視線上の一点には、その一点を中心とするようなモノから広がる空間を想定することができますよね。言い換えれば、次元観察子ψ5〜ψ6という球空間はそれぞれが無数のψ3〜ψ4の集合で構成されているということなのです。
さて、おそらく上でのNC上でのψ5とψ6のイメージは分かりづらかったと思いますので、ここでもう一歩突っ込んで、次元観察子ψ5とψ6の球空間がどのようなカタチを持っているかを調べてみましょう。ψ5の球空間の中心点はNCを見て分るように+∞と−∞の重合点になっています。これは観測者の位置そのものです。この重合のイメージを取りあえず実際の空間上で作ってみることにしましょう。すると、ちょっと奇妙な描像ですが、それはおおよそ次のようなイメージになってきます(下図3参照)。
目の前にモノがあります。その背後に遥か彼方まで延びる無限の長さの直線があります。そして、その直線が無限遠点(−∞)に達したところに自分がいます。しかし、そこに見える自分は自分の後頭部です。このことを想定した上でグルっと回ってみましょう。すると、回っても回ってもその視線の彼方にやはり自分の後頭部が見えることになります。つまり、次元観察子ψ5という球空間は観測者が知覚球面を形作ったときには、その球面上のどの方向にも観測者自身の後頭部が見えるような構造になっているということです。はて、はて?何のこっちゃ?——つづく
By kohsen • 時間と別れるための50の方法 • 0 • Tags: 内面と外面, 無限遠