時間と別れるための50の方法（16）

●4次元空間への脱出口
　「時間と別れるための50の方法」とタイトルを銘打って書き進めてきたこの駄文も、もう（16）まで来てしまいました。肝心の時間についての話が一向に出てこないじゃないかと怪訝に思っていらした方も多々いることでしょう。ようやくです。ようやくこれで時間を含めた4次元という次元（4次元時空と4次元空間）の本質についてヌース的な視点から話す準備が整いました。ここからは今まで以上に頭の柔軟性が必要になります。OCOT情報を交えながらじっくり進めましょう。

　モノから広がっている3次元空間の方向性はシリウスでは何と呼ぶのですか？
　垂子（スイシ）です。垂子とは線です。
（シリウスファイル）

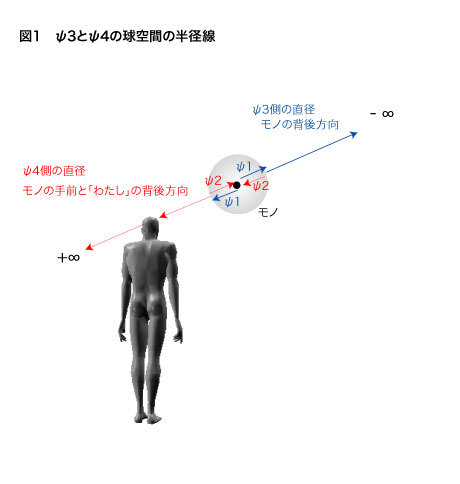
　まずは、今まで説明してきたψ3とψ4の球空間の半径が持つ互いの関係を正確に描いておきます。

　この図から、ψ3の半径部分は観測者から見てモノの背後方向に延びている直線に対応することが分ります。一方、ψ4の半径部分の方は、モノの手前にいる観測者自身の方向、さらにはそこをも突き抜けて、観測者の背後側へと延びている直線に対応しているのが分ります。今一度、皆さんもその二つの方向性の違いを確認してみて下さい。

　すると、ψ3の半径が指し示す方向は正面方向にあるので「見えます」が、ψ4の半径の方向性はモノの手前側に向いており、まずは「わたし」の顔面方向、さらにはそれを突き抜けた後は「わたし」の背面方向となって、共に「見えない」ことが分ります。この「見える」「見えない」が「人間の外面」と「人間の内面」の違いです。僕は外面を「現実的なもの」、内面を「想像的なもの」とよく言い換えるのですが、これは、前は見える、という意味において現実ですが、後ろは見えないという意味において、つねに想像でしかないからです。

　モノから広がる3次元空間の概念は実は人間の内面=ψ4の球空間にしかあてはまらない。というのが前回の内容でした。では、現実として目に見えている外面=ψ3の球空間は一体どこにいったというのでしょう。
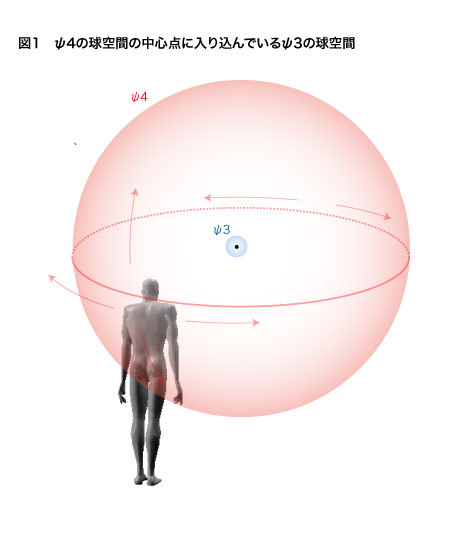
　ここで、もともとψ3の球空間が2次元射影空間を作り出すための球空間であった、ということを思い出す必要があります。モノの背景面方向には確かに、無限遠方へと延びている線分が感覚化されています。しかし、現実としての知覚正面上ではその線分上の点はすべて一点で同一視されているというのが分かります。つまり、射影空間上ではψ3の球空間の中心点（光学中心と言います）と無限遠方は同じものになっているという言い方もできるのです。つまり、無限遠の長さの半径が無限小の長さに潰されているということです。そうした線が回転するのですから、ψ3はその中心にある微小な球体に縮まっていると考えられます。ψ4に包含されてしまったψ3とは何と中心点近くまで入り込んでいるわけです。『人神/アドバンスト・エディション』では、この入り込みを空海のいう重々帝網という仏教概念を使って即身化のルートと呼びました。微塵のミクロ世界にも、マクロが映り込んでいるというわけです。ライプニッツの言葉を借りれば、これはモナドです。

　こうして説明しても、見えている世界がミクロ世界？そんなバカな、と思う方がほとんどだと思います。とにかく、実際に皆さんの身体を使ってこの様子を確かめてみて下さい。前回示したワークで言えば、バスケットボールの周囲を回転していくときに、その中心とその背後方向に延びている無限遠へと延びている線が、現実には点のように見えていることを確認しながら、ゆっとりとバスケットボールの周囲を回ってみればいいだけです。どうでしょうか。ボールの背景面上で次々と遷移していく無限の彼方にまで延びているはずの視線の突端はボールの中心点とピタリと一致して、点にしか見えないのが分りますね。知覚的事実としてこれは否定のしようがありません（下図1参照）。

「神が聖母マリアの胎にひそかに宿り給うたとき、そのとき点が円環を内包したのだ。」
　こちらも、ヌースではもうおなじみの引用（『シリウス革命』205ページ）ですが、これは16世紀に活躍したオランダの建築家シェフラーという人の言葉です。この言葉は人間の空間認識の反転が、世界に創造者を再来させる、ということを意味しています。マリアの胎にひそかに宿り給う神………受胎告知ですね。この「ひそかに」というところがミソです。光の救済なんてものはそんな派手なものとしてはやってこない。人間の内面に堕ちた光のかけらをそっと物質（マテリア）の中心に差し戻してやること。そこから光の目醒めが始まります——つづく