3月 27 2008
時間と別れるための50の方法(4)
●物理学におけるアルケー(ホーキング=ハートルの無境界仮説)
さて、奥行きの4次元としてのアルケーについて語るのは、ここで一旦止めにして、現代宇宙論においてこの「アルケー(宇宙の始まり)」がどのように語られているのかを見てみることにしましょう。現代宇宙論の主流は周知のようにビッグバン理論にあります。ビックバン理論によれば、宇宙は約137億年前に特異点という極微の点的存在から突如、大爆発を起こして誕生し、今尚、膨張し続けていると言われています。しかし、この宇宙の開始点となっている特異点という存在は物理学者たちにとっては甚だ目障りな存在です。特異点というのは、アインシュタインの宇宙方程式から必然的に導き出されてくるものらしいのですが、そこではエネルギー密度や温度が無限大になってしまうのです。そのため、微分方程式が計算不能になってしまい、物理法則がすべて破綻してしまいます。宇宙がどのようにして始まったのか理性で把握したい物理学者にとってはやはり、これはのっぴきならない事態です。
この厄介物の特異点を何とか回避できないかものかと考えたのが、あの車椅子の天才と言われたS・ホーキングです。ホーキングは1983年にJ・ハートルとともにに「無境界仮説」という奇抜な仮説を発表します。無境界仮説は、この実時間の宇宙の開始時に虚時間宇宙(量子重力期とも呼ばれます)の存在というものを考え、ビッグバン以前の宇宙がどういう状態にあったかその有り様を数学的に示したものでした。これは虚時間宇宙を導入すると、相対論的に区別されていた時間と空間の区別が無くなり、特異点自体が消えてしまうからです。
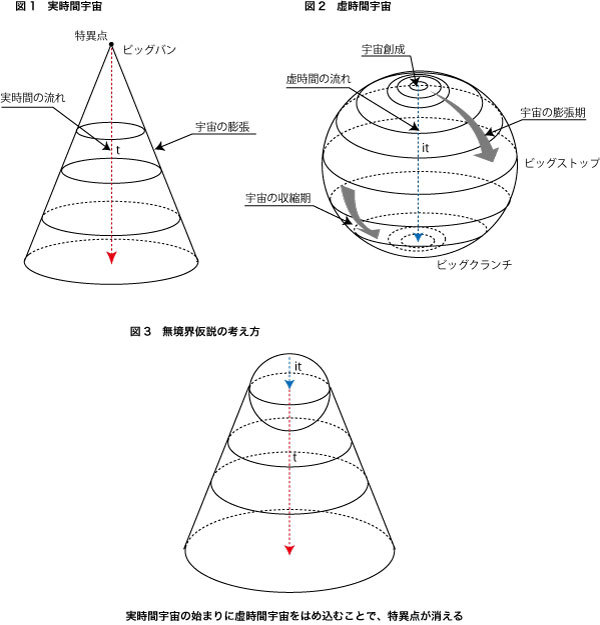
このへんの事情を分りやすく説明すると、おおよそ下のような直観的な図で説明することができます。図1で示したのが膨張宇宙と思って下さい。時間tと共に膨張していく姿をこの図では円錐形で示しています。円錐形の先はつんととんがっていますが、この先端点が特異点と考えましょう。
ここで、時空における時間の項を虚数にすると、数式上、次のようになります。
ローレンツ変換の不変量である4次元距離をsとすると、
s^2= (x^2+y^2+z^2)+(ict)^2
ここで実時間tの代わりに虚時間itを代入すると、
s^2=(x^2+y^2+z^2)+(ic(it))^2
となり、 Sを1と置いて整理すると
x^2+y^2+z^2+ (ct)^2 =1
という式になってしまいます。この式は4次元ユークリッド空間上での原点から1の距離を持つ3次元球面を表す式と何ら変わるところはありません。つまり、時空を表す式に虚時間を代入すると、時間は空間と区別がつかないものになってしまうということです。
この実時間から虚時間への変換(物理学ではウィック回転と呼ばれています)は、4次元方向の計量を反転させることに対応しているとも言えますが、大ざっぱな幾何学的イメージとしては円錐状の時空を球面状に丸めることに対応しています(図2参照)。要は、虚時間の導入によって、4次元の円錐が4次元の球体に変換されてしまうということです。こうした球体状の時空が実時間宇宙の始まりには存在していたのだ、というのがホーキング=ハートルによる無境界仮説の骨子です。
時空が球体状のカタチをしていたとすると、宇宙の始まりは、ちょうど先の尖った鉛筆の芯をボールペンの芯に変えたときのように、円錐の頂点の先が丸い球面状になっていたことを意味します(図3参照のこと)。このような考え方から、ホーキングは宇宙の始源では、始まりも終わりもないようなエンドレスかつシームレスな世界があったのだと言うのです。とすると、このアルケーとしての球面世界は、ビッグバンが起こった場所とビッグクランチの場所が繰り返し相互に繰り返しているような宇宙イメージになってきますし、さらに言えば、この球面上ではどのような対極点も同等なものなので、虚時間宇宙上ではどの場所を取っても、宇宙の始まりであり、終わりでもあることになります。これは仏教で言う「無始無終」の宇宙像ととても似ていますね。時空上のあらゆる場所、つまり、いつでも、どこでも、そこには無始無終の久遠の世界があるということです。
「久遠とははたらかさず・つくろわず・もとのままという義なり」
「久遠は今に在り、今は即ち久遠なり」
(by 日蓮)







2008年3月27日 @ 22:54
コウセンさん、こんばんは。
物理学者フリーマン・ダイソンは20年以上も昔にこんなことを言っているそうです。
「私は小さな夢を持っている。なんの事実も証拠もあるわけではないが、『21世紀のある日、物理学者が、宇宙の構造の中に思いもよらない方法で組み込まれているモンスター単純群に遭遇するだろう』と。」
散在型単純群であるモンスター群の次元数196,883は、23次元球面S^23上のリーチ格子の格子点の個数196,560(リーチ格子は第1層がなく第2層から)と関係が深いそうです。
ちなみに、24次元の正単体は正25胞体、立方体は正48胞体、正軸体は正16,777,216胞体です。
また、例外型単純リー群であるE8群の次元数248は、7次元球面S^7上のE8格子の格子点の個数240と関係があるそうです。ちなみに、8次元の正単体は正9胞体、立方体は正16胞体、正軸体は正256胞体です。
このリーチ格子の格子点の個数を、こんな数の関係式にしてみました。
(地球の歳差周期の年数)÷(3次元の接吻数)=(24次元の接吻数)÷(14次元回転群の自由度)=(8次元E8格子の第2層の点の個数)=(黄道12宮1星座分の年数)
(ただし、(地球の歳差周期の年数)=(プラトン周期の年数)、(14次元回転群の自由度)=(1~13までの数の総和)、(3次元の接吻数)=(3次元A3格子の第1層の点の個数)、(24次元の接吻数)=(24次元リーチ格子の第2層の点の個数))
25,920÷12=196,560÷(1+2+3+4+5+6+7+8+9+10+11+12+13)=2,160
地球の歳差周期は、地球の自転軸の傾きと関係があり、地球の自転と言えば1日=24時間。
なんだか、関係式の数値たちが、ヌースっぽい数値に見えてくるでしょう?
その上、このリーチ格子を構成する196,560個の格子点の内訳196,560=97,152+1,104+98,304が面白いです。わかりやすいように、距離を1ではなく、32、つまり、4^2+4^2とすると、まず、97,152個の点は、2^2+2^2+2^2+2^2+2^2+2^2+2^2+2^2+2^2=4^2+4^2という配置なので、(8,2)型ミンコフスキー空間のローレンツ格子と見れます。また、1,104個の点は、4^2+4^2=4^2+4^2という配置なので、(2,2)型ミンコフスキー空間のローレンツ格子と見れます。最後に、98,304個の点は、(-3)^2+1^2+…+1^2=4^2+4^2という配置なので、(24,2)型ミンコフスキー空間のローレンツ格子と見れます。ローレンツ格子ということは、光線と関係し、時空距離がゼロとなるヌル・ベクトルです。それぞれグループ別に、10次元ローレンツ格子、4次元ローレンツ格子、26次元ローレンツ格子と呼ぶと、何だが、最初のグループは右回りの超ひもの次元、最後のグループは左回りのボソンひもの次元と関係するように思えます。すると、真ん中のグループは何でしょう?何か蝶番の役割でも果たしているのでしょうか?
どうも、格子の階層構造、つまり、奥行き的な構造と、時間成分の個数とはどうやら関係が深そうです。ヌースのPSO回路などでは26次元空間と10次元空間の構造の関係はどう見るのでしょうね?
2008年3月28日 @ 08:19
ちょっと、ヌースにおけるコード化(エンコード)、脱コード化(デコード)の基本構造が見えてきたように思います。
まず、ψ7~ψ8の作用としてψ1~ψ2,ψ3~ψ4,ψ5~ψ6までをも含んで4ビットとして「実体ビット」構成(コード化)をしてきますが、ψ13~ψ14の作用としてψ9~ψ10,ψ11~ψ12までをも含んで、さらに4ビットを付加して「検査ビット」構成(脱コード化=コード解析して再コード化する)をしてきます。これによって、合計8ビットのデータ構造が生成されます。下位4ビット分が四元数として機能し、上位4ビットまで含んで八元数として機能するのだと思います。私が考えるには、20世紀末までにこの世界の情報は「実体ビット」構成として完成し、既にこの世界の情報はもう「実体ビット」としてではなく、「検査ビット」として使われ始めていると思います。ある意味、コードとしては「使い捨て」の時代に入ったわけです。私がここで、「実体ビット」構成と呼んでいる部分で、リー群でもある3種類の球面構造S^0,S^1,S^3を構成します。しかし、ここまでで構成される部分は、私たちにとっては互いの「視線」(眼差し)の構成までしか行きません。まだ、満足な「形」すらできないわけです。上位の影として「形」(最初は「正三角形」)が構成されるのは、「検査ビット」構成が始まる前後からだと思います。ここから実際の「知覚正面」への「平形投影」が行われ、「ベクトル平衡体」を構成していくわけです。しかし、これすらも実際には4次元の自己双対超立体である「正24胞体」の投影、つまり、切断面的な図形でしかありません。ちなみに、「正24胞体」はその内部構造に、4次元の正8面体に相当する「正16胞体」と、4次元の正6面体に相当する「正8胞体」を含みます。別の言い方をすれば、ψ1~ψ8は「視線」の反復構造=「神経症」構造(パラノ構造)を作り、ψ7~ψ14は「視線」に基づく自由な組み立て過程としての構造=「分裂症」構造(スキゾ構造)を作っているとも言えるかもしれません。
ところで、『2001年宇宙の旅』で有名なアーサー・C・クラークさん、この3月19日に亡くなられたようですね。人類はまだ『幼年期の終り』を迎えていないというのに…。直接関係ありませんが、ちょっと宇宙話題つながりということで。
2008年3月28日 @ 15:25
Φさん、立て続けにコアな書き込みです。
モンスター群なんかのレベルになると、完全にホールドアップです。
>ヌースのPSO回路などでは26次元空間と10次元空間の構造の関係はどう見るのでしょうね?
詳しいところはまだ分りませんが、直観的には「次元の対化における中和」に存在する次元数と、同じくその等化における次元数の関係のように思えます。ボゾンは精神の残響として残された付帯質の変換のカタチの力ではないかと考えています。