差異と反復………7

単に3次元の広がりとしてしか認識されていないこの空間には反転したもう一つの3次元空間が重畳している。一つは客体の場（人間の内面）となり、そして、もう一つは主体の場（人間の外面）となっている。これがヌース理論がこの十数年の間言い続けてきていることだ（前者が次元観察子ψ4、後者がψ3に対応する）。

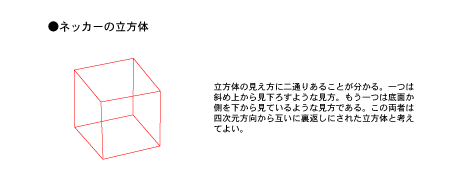
　この二つの空間を可視的なイメージに置き換えることは可能だ。それには下図に示したよう正六面体のフレームワークを紙の上に描いてみるといい。この正六面体を3次元立体として見ると二種類のものがイメージできるはずだ。そして、それらは相互に反転していることが分かるだろう（ネッカーの立方体）。対象認識にはこうした２つの空間の存在が暗躍しているのだ。

　このような描像を用いて対象界面をイメージしてみると、そこには対象の内壁と外壁が同居している様子が朧げながらも浮かんでくるのではないかと思う。つまり、反転した空間を考慮に入れると、モノと空間の境界面はその内部と外部それぞれの同一性を無効にするような形で存在させられているということになる。つまり、内部=外部、外部=内部という関係を成立させているということだ。内部と外部の向き付けが不能な面。。こうしたイメージはあのおなじみのメビウスの帯が提供してくれるのを僕らは知っている。実際に、前回紹介した2次元射影空間RP^2の切り口は縁のないメビウスの帯になることが幾何学的には分かっている。

　つまるところ、僕らの対象認識においてモノの内部と外部を差異化させているのは、このメビウスの帯的な空間の捻れなのだ。これは別の言い方をすれば内部方向と外部方向を等化している力、つまりヌースでいう「最小精神」のカタチである。その等化に反映されているのが中和としての3次元空間だ。内部と外部の間に捻れがあるにもかかわらず、それが見えないと、その捻れ自体が境界のように見えてしまう。それがおそらくモノの界面の現出に潜むからくりである。トポロジカルな言い方をすれば、モノと空間の境界面とは4次元空間における2次元の結び目と言えるのかもしれない。僕らが慣れ親しんでいるのはひものような1次元図形の結び目だが、この結び目を作るには最低3次元の空間が必要になる。ひもの結び方を知っている者にとっては、結び目ができていようとそれは単なる一本のひもにすぎない。しかし、結び目が何か知らない者にとっては、それは奇妙なこぶのように見えてしまう。それと同じで、モノ概念は2次元の結び方を知らない3次元意識だけに存在するものなのだろう。

　メビウスの帯の場合、捻りとは帯の幅方向の180度回転に当たるが、3次元空間の場合、捻られたのは無限小と無限大方向相互の180度回転である。このとき、人間が3次元認識の中で「点」と呼んでいたものは、無限大の球面（平面）のようなものに置き換わる。つまり、無限小と無限大の対称性が形作られたということだ。そこが背景正面としてのψ3の位置である。当然、その捻れが見えていないものが反映としてのψ4の位置となる。ψ4はψ3が持った捻れをψ1とψ2の境界のようなものに感じ、等化という回転（捻り）の働きが裏で暗躍しているがゆえに、ψ1（無限大方向）とψ2（無限小方向）の間を反復してしまうのだ。
　こうして、等化=差異、中和=反復というヌース理論の文脈からの「差異と反復」の最も基本的な鋳型が幾何学的に構成されたことになる。ということで、次で終わろうかな。。長くなってしまった。。