原子の基礎

認識にモノ概念が成立するための空間構造を幾何学的にもう少しはっきりさせておこう。
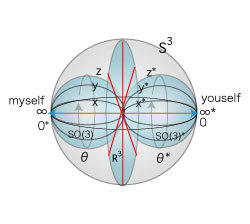
　世界には無数のモノがある。今、わたしの周囲には灰皿や本やPCや外の木々や電信柱などが散在している。こうしたモノの多数性は前回示した4次元球体の構造の中でどのように対応させればよいのか——この対応を作るためには、上図のように4次元球体の内部に二つの内接する3次元球面θ、θ*をセットするとうまくいく。これら二つの3次元球面はそれぞれが自己と他者に見えているモノからx,y,z方向に広がっている3次元空間を球面状に丸めたものである。球面θでは∞側が一点で同一視され、球面θ*では∞*側が同じく一点で同一視されている。これらは言うまでもなく、自己と他者それぞれにおける主体としての位置だ。モノの3次元の並進方向は、この球面θ、θ*上のそれぞれの3つの円環の回転と考えるといい。自他がモノの並進方向を意識するとき、球面θとθ*上の円環は同期した鏡像回転を起こしている。SO(3)とSO(3)*で表されたこの二つの3次元球面の4次元方向を軸とする自転はモノから広がるx,y,z軸のすべてを観測者の「前」が等化している状態を意味する。つまり、観測者がモノの周囲をグルグルと周ったときに見える、モノの中心点とその背後方向に位置する無限遠の天球面を同一視させる運動を意味しているということだ。以上のような対応を考えれば、3次元空間上に存在するすべてのモノ（位置）を、このθとθ*の接点の位置Pに対応させることが可能となる。

　以上の考察から、意識がモノ概念を形作るためには少なくともSO(4)対称性という条件が必要であることが分かるだろう。ただし、このときに概念化されるモノとは普通にいう客体としてのモノのことではないことに注意しよう。何度も言うようだが、SO(4)対称性は人間の外面に形作られるものなので、これは客体ではなく、集合主体としての役目を持っている。普通にいうところの客観的なモノとは人間の内面認識におけるモノのことであり、それはSO(4)ではなく、おそらくSO(1.3)で表されるローレンツ変換対称性として解釈されるのではないかと思う。

　SO(4)対称性と言っても多くの人はピンとこないと思うので、これをSO(3)×S^3という形に書き直してその物理的意味を考えてみる。3次元球面S^3は数学的には2次元複素ユニタリー群SU(2)と同相とされる。これは複素2次元ベクトル空間上での回転群のことだ。3次元球面S^3の双方向の自転によって生じている軸を電子のアップスピンとダウンスピンとすると、SO(4)においては、この両スピンがさらにS^3=SU(2)をなぞるように回転しているというイメージが生まれてくる。これは前回も言ったように一つのモノに対する無数の他者の眼差しに相当する。つまり、無数の眼差しの一点への集中とは、特定の自己のアイデンティーを決定している電子のスピンが、モノから広がる3次元空間上の様々な位置に配位されている様子と解釈するわけだ。このようにスピンがさらに回転しているような空間は物理学ではアイソスピン空間と呼ばれる。つまり、電子のスピンは3次元球面S^3の自転軸として出現しているのだが、そういった自転軸をさらにS^3=SU(2)に沿って回転させ、それら3方向の回転をさらに一つの方向に統合しているような上位の回転軸を想像すればいい。言うなればスピンの上位にあるメタスピンのようなものだ。その軸の双方向がアイソスピンである。物理学ではアイソスピン-1/2が陽子で、+1/2が中性子とされる。

　これらの文脈から陽子と中性子の実体とは何かが描像できる。一言で言えば、それは自他における「前」の総体と「後」の総体の関係だ。これはヌース理論の文脈では集合主体の原器と集合客体の原器を意味する。そして、これら両者は実のところ客観的なモノ概念と時空全体の関係となって現れてくる。つまりこういうことだ——目の前に幾ばくかのかさばりを持ったモノがある。その周囲に空間の広がりとしての時空がある。そして、それを見ている「わたし」がいる。それらをすべて概念として解釈すると、その概念のカタチがそれぞれ陽子、中性子、電子に対応していることになる。重水素を作る材料がこれで揃ったというわけだ。