3月 27 2008
時間と別れるための50の方法(4)
●物理学におけるアルケー(ホーキング=ハートルの無境界仮説)
さて、奥行きの4次元としてのアルケーについて語るのは、ここで一旦止めにして、現代宇宙論においてこの「アルケー(宇宙の始まり)」がどのように語られているのかを見てみることにしましょう。現代宇宙論の主流は周知のようにビッグバン理論にあります。ビックバン理論によれば、宇宙は約137億年前に特異点という極微の点的存在から突如、大爆発を起こして誕生し、今尚、膨張し続けていると言われています。しかし、この宇宙の開始点となっている特異点という存在は物理学者たちにとっては甚だ目障りな存在です。特異点というのは、アインシュタインの宇宙方程式から必然的に導き出されてくるものらしいのですが、そこではエネルギー密度や温度が無限大になってしまうのです。そのため、微分方程式が計算不能になってしまい、物理法則がすべて破綻してしまいます。宇宙がどのようにして始まったのか理性で把握したい物理学者にとってはやはり、これはのっぴきならない事態です。
この厄介物の特異点を何とか回避できないかものかと考えたのが、あの車椅子の天才と言われたS・ホーキングです。ホーキングは1983年にJ・ハートルとともにに「無境界仮説」という奇抜な仮説を発表します。無境界仮説は、この実時間の宇宙の開始時に虚時間宇宙(量子重力期とも呼ばれます)の存在というものを考え、ビッグバン以前の宇宙がどういう状態にあったかその有り様を数学的に示したものでした。これは虚時間宇宙を導入すると、相対論的に区別されていた時間と空間の区別が無くなり、特異点自体が消えてしまうからです。
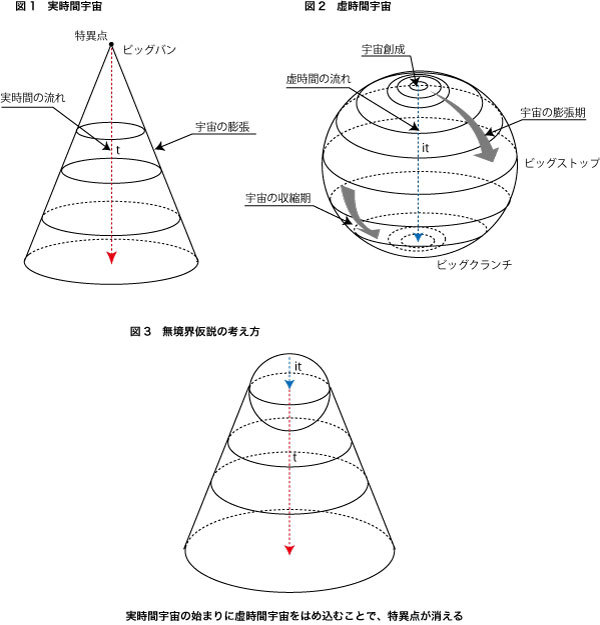
このへんの事情を分りやすく説明すると、おおよそ下のような直観的な図で説明することができます。図1で示したのが膨張宇宙と思って下さい。時間tと共に膨張していく姿をこの図では円錐形で示しています。円錐形の先はつんととんがっていますが、この先端点が特異点と考えましょう。
ここで、時空における時間の項を虚数にすると、数式上、次のようになります。
ローレンツ変換の不変量である4次元距離をsとすると、
s^2= (x^2+y^2+z^2)+(ict)^2
ここで実時間tの代わりに虚時間itを代入すると、
s^2=(x^2+y^2+z^2)+(ic(it))^2
となり、 Sを1と置いて整理すると
x^2+y^2+z^2+ (ct)^2 =1
という式になってしまいます。この式は4次元ユークリッド空間上での原点から1の距離を持つ3次元球面を表す式と何ら変わるところはありません。つまり、時空を表す式に虚時間を代入すると、時間は空間と区別がつかないものになってしまうということです。
この実時間から虚時間への変換(物理学ではウィック回転と呼ばれています)は、4次元方向の計量を反転させることに対応しているとも言えますが、大ざっぱな幾何学的イメージとしては円錐状の時空を球面状に丸めることに対応しています(図2参照)。要は、虚時間の導入によって、4次元の円錐が4次元の球体に変換されてしまうということです。こうした球体状の時空が実時間宇宙の始まりには存在していたのだ、というのがホーキング=ハートルによる無境界仮説の骨子です。
時空が球体状のカタチをしていたとすると、宇宙の始まりは、ちょうど先の尖った鉛筆の芯をボールペンの芯に変えたときのように、円錐の頂点の先が丸い球面状になっていたことを意味します(図3参照のこと)。このような考え方から、ホーキングは宇宙の始源では、始まりも終わりもないようなエンドレスかつシームレスな世界があったのだと言うのです。とすると、このアルケーとしての球面世界は、ビッグバンが起こった場所とビッグクランチの場所が繰り返し相互に繰り返しているような宇宙イメージになってきますし、さらに言えば、この球面上ではどのような対極点も同等なものなので、虚時間宇宙上ではどの場所を取っても、宇宙の始まりであり、終わりでもあることになります。これは仏教で言う「無始無終」の宇宙像ととても似ていますね。時空上のあらゆる場所、つまり、いつでも、どこでも、そこには無始無終の久遠の世界があるということです。
「久遠とははたらかさず・つくろわず・もとのままという義なり」
「久遠は今に在り、今は即ち久遠なり」
(by 日蓮)







6月 10 2008
時間と別れるための50の方法(12)
●再度、人間の外面と内面
さて、ここで、人間の内面と外面という空間概念を分りやすくするめに、『人神/アドバンスエディション』でも示した図を引っ張ってきてみましょう。下図1がそれです。
『アドバンス・エディション』では「人間の外面」を見える空間、「人間の内面」を見えない空間として紹介しました。この図を再度、ご覧になってみて下さい。人間が空間上の何か一つの対象を認知するとき、そこには「図」としてのモノの表面側と、「地」としての背景空間側が存在しているわけですが、この図ではそれらがともに人間の外面としてブルーの実線で描かれているのが分ります。しかし、互いの面の関係を見てみると、それらは凸面と凹面の関係になっています。こうした凹凸の反転関係から、モノの内部と外部の空間は、3次元的なものとして捉えたときには、同じ3次元空間ではなく互いに反転した関係として捉えられるべきだ、というのが『アドバンスト・エディション』で主張した内容です。
というのも、僕らの一般的な空間把握(人間型ゲシュタルト)はこうした反転概念を通してモノとその背景空間を捉えることができていないからです。どういうことかと言うと、前回もお話ししたように、僕らはモノの外部の空間にも尺度を与えて、モノの内部性として感覚化している「大きさ」という概念で空間を把握することがクセになっているので、対象の背景にある空間領域もまたモノの内部空間をそのまま単純に拡大させていった空間と同じ空間として見なすのが常識となっています。このような空間概念でモノの背景空間が捉えられてしまうと、モノの背景面として見えている面は概念としてはモノの内壁(実際に見えているモノの表面のウラ側)を構成している側の面と全く同じ面の延長として見なされることになるのが分るはずです。
はてはて、このような空間認識の在り方の一体どこがまずいの?と疑問に持たれる方もおいででしょうが、ここで、よぉ〜く、よぉ~く考えてみて下さい。しつこいようですが、「よぉ〜く」です。ヌース的に言えば、ここが変換人の意識(顕在化)と人間の意識(そのまま潜在化)の分岐点になります。OCOT風に言えば、ムー次元とアトランティス次元の分岐点なのです。どひゃー。えらいこっちゃ。
モノの背景面は果たしてほんとうにモノの内壁をそのまま拡大させていった面となっているでしょうか?この問いに対する答えは実際に見えている空間を2次元の射影空間として捉えるとそれなりに分ってきます。
再度、上図1を見てみましょう。この図では読者の空間イメージを喚起するためにモノ、観測者、そして、それらが配置されている空間の諸関係が真横から見た様子として図示されています。しかし、実際、観測者の位置に自分が立ち、そこからモノや背景空間を見ると、その様子は下図2に示したように、ただ、モノの表面部分(図)と背景空間(地)があるだけの状態となります。
ここでは、モノとその背景空間が織りなす空間はペッタンコに潰されていて、幾何学的には平面状の形状として表されているのが分ります。つまり、いつも言ってるように視線上にある奥行き方向がすべて一点同一視され、2次元の面的な空間になっているわけです。
ただ、2次元と言っても、ここでいう2次元は普通の2次元ユークリッド空間とは全く違う性質を持った2次元です。こうした空間は幾何学的には2次元射影空間と呼ばれています。つまり、知覚正面としての視野空間は3次元空間というよりも、2次元射影空間の性質を持っているということです。
2次元射影空間の幾何学的な定義については『アドバンスト・エディション』の脚注部分に書いているのでここでは割愛しますが、大事なことは、視野空間を2次元射影空間と見なした場合、視線上で知覚されているモノの表面上の一点とその背後にあると想像されている背景空間上の一点は同じものとして見なされる、ということです。つまり、最初に示した図1で言えば、点Aと点Bは同一視されているということを意味します。このことが3次元的にどういう意味合いを持っているか考えるためには、モノを中心として視線自体の回転を行なってみるといいでしょう。つまり、一つのモノを見ながら、その見つめている視線をモノを中心に回転させていってみるのです。
そうすると、回転とともに視線上に捉えられているモノの表面上の一点一点は、同じく、モノの背景面上の一点一点と一対一で対応関係を持っていきながら遷移していきます。とすると、視線の回転によってなぞられていくモノの表面を構成している球面(凸面側)と、モノの背景面としてなぞられていく球面(凹面側)とは、その光学中心(認識されているモノの中心点)で相互に反転している関係があるということになります。つまり、モノとして認識されている球体の内部と背景として認識されている外部の3次元性には互いに反転関係が隠されているということです。このような認識から、ヌース理論では、知覚正面に捉えられているモノの背景面はモノの表面が反転して現れた面であって、決してモノの内壁が拡大されて現れたものではないと考えるのです。
では、実際にモノの内壁が単純に拡大されていった面はどこに感覚化されているのでしょうか——それは簡単です。知覚正面側ではなく、知覚背面側です。目の前のモノがどんどん拡大されてくるイメージを作ると、ある時点でそのモノのイメージが観測者自身を包む込んだイメージに切り替わります。このときモノの内壁だったところは、自分の背中方向に感覚化されるようになります。つまり、後ろ、です。これは、このシリーズでもお話してきたように、モノの手前にいる自分や自分の顔をイメージしている鏡像空間です。つまり、目の前のモノが自分を包む込むイメージが生まれたときには、意識が人間の外面から内面に反転させられているのです。言うまでもなく、そうしたイメージで捉えられている空間は実際に見えている空間ではありません——つづく。
By kohsen • 時間と別れるための50の方法 • 0 • Tags: アトランティス, ムー, ユークリッド, 人間型ゲシュタルト, 人類が神を見る日, 内面と外面