3月 25 2007
水素原子の描像
今日はちょっと難しい話。
原子の本質を理解する意味でとても重要な議論を、現在、ヌース会議室上でΦさんと交わしている。Φさんはすでにヌース理論が提供しているケイブコンパスモデルの内容をほぼ理解されている。その上で、物理数学の専門的な知識との擦り合わせを単独で進めてられているようだ。Φさんの分析は、ヌース的に見て実のところとても鋭い。僕自身、物理学の知識が全然不足しているので追いかけるのが大変だが、観察子の描像を具体的に意識に浮上させていく上で大変有用なものとなっている。そこで、今日書いたΦさんへのレスをこちらのブログにも転載することにした。
前後関係もなく、具体的な解説も端折られているので、ここだけ読むとちょっと難しいかもしれないが、ヌース理論が主張したいポイントはただ一つ。水素原子とは人間が持った概念の構造であるということだ。それも、主観、客観、モノ、観測者といった、認識の起点となるべき基礎概念の構成であるということ。こうした考え方で原子を捉えられるようになってくれば、これからの人間は、精神即物質という世界観のもと、全く違う生き物に変容していける可能性がある。——それを作れ。そうすれば彼はやってくる。。。
Φさん、とりあえず、また一つだけに絞らせて下さい。
——おそらくこの離散値の由来はSpin(1)=O(1)ではないかと思います。軌道角運動量の演算子をL、スピン角運動量の演算子をS、ディラック行列をα、空間推進(つまり、量子力学的運動量)をp(いずれも3次元ベクトル風)とすれば、ハイゼンベルグの運動方程式より、
dL/dt=+(α×p)
dS/dt=−(α×p)
が成り立ちます。私の考えでは、αは4次元の時空的捩れを表現するものであり、dL/dtは「時空の推進」、ds/dtは「時空の反推進」と考えております。dL/dt+dS/dt=d(L+S)/dt=0ですから、この2者の「相殺」により、「全角運動量」J=L+Sが保存されることになります。「角運動量」は「空間の回転」に対する保存量ですから、「全角運動量」は「時空の回転」に対する保存量と呼んだ方がいいのかもしれません。——以上、Φさんの書き込みからの抜粋。
Φさんの物理数学的知識からくる構造分析をケイブコンパスに当てはめてみました。現在、僕が持っている描像とかなり符合する点が多いようです。かなり勇気づけられます。
ROMの皆さんを意識して、分かりやすく図で説明します。
ここでは電子のスピン角運動量と軌道角運動量との関係を考察しているわけですから、当然、電子はすでに核子(この場合、もっともシンプルに陽子1ケと考えましょう)に捕捉されています。ということは、陽子を形作った対称性がまず先に存在していて、そこに、新たに電子が加わっているという構図について話をしていることになります。
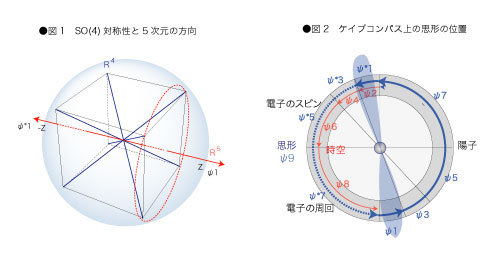
陽子はご存知の通り、ケイブコンパス上ではψ7として表現されます。ψ7が持つ対称性は今のところS0(4)です(SO(3)対称性をスピノールと見れば、SO(4)はSO(3)×S^3なので、SU(2)とも解釈できるのではないかと思います)。SO(4)対称性はプラトン座標では、正六面体の4本の体心立方軸(√3エッジ)をすべて等化するような回転として現れると考えています。すると、このときの回転軸は、今度は面心立方方向の一本の軸として出現してくることが分かります(下図1)。この方向がヌースが5次元と呼んでいるものの方向です。この5次元における双方向性、言い換えれば、SO(4)群の中心としての(Z,-Z)がO(1)=Spin(1)を観察しているのではないかと考えています。ヌースでいう「表相の等化」です。
「表相の等化」は知覚正面上における前後(表裏)を、左右と見なせるような認識の視座を意識に用意してきます。分かり易く言うと、実際にはモノの表と裏に見える部分を、意識にはそれを真横から見てあたかも左右方向のように見立てている想像力が含まれているということです。この想像力を提供している位置が表相の等化の位置に当たります。事実、幾何学認識の問題として、(Z,-Z)は左右方向(もしくは上下)でしか認識の対象に成りませんよね。ケイブコンパス上ではこの位置は下図2のように表すことができます。これは陽子のアイソスピンとも言えるのではないかと考えています。
さて、ここから、陽子による電子の捕捉が始まるわけですが、この段階で捕捉される電子はψ5(自己側の知覚球面)ではなく、ψ*5(他者の知覚球面=他者を規定している空間のカタチ)の形を模索している自己側の意識のカタチになっていると思われます。つまり、客観的モノ概念(ψ7=陽子です)を挟んで、ψ5とψ*5を対化として見れる視座の獲得です。
しかし、これだけでは、電子=ψ*5のカタチは軌道角運動量を持ち得ません。つまり、陽子の周囲を回っていないということです。電子を陽子回りに周回させるためには、今度は3次元空間(S^3上)に散在している無数の他者の位置を用意する必要があるのではないかと思われます。つまり、特定の他者の知覚球面ではなく、いろいろな場所に存在する無数の他者の知覚球面を自己側がイメージできるような自由度を考えなければならないということです。意識によるこの自由度の獲得が電子の周回の意味に対応させることができるのではないでしょうか。これは別の言い方をすれば、観測対象と観測者全員が一つの同一化した空間に投げ込まれている状態の認識と同じですから、結局は客観的時空のイメージを形作るための能動力として解釈することが可能です。つまり、陽子が客観的モノ概念の形成力だとすれば、その周囲を巡る電子の公転とは客観的時空概念の形成力ではないかということです。こうして、陽子の周囲を周回する電子の幾何学的描像が、客観的時空上の客観的モノという概念と一致してくることになります。
以上のような描像から、「全角運動量が時空の回転に対する保存量である」というΦさんの意見には納得が行きます。ヌース的には「全角運動量」とは、自転角運動量と軌道角運動量を足し合わせたものですから、結局のところψ7がψ*7のカタチを模索している意識の状態に当たります。ψ*7はψ8を観察する働きを持っています。ψ8はローレンツ変換対称性です。ここでΦさんが言われる「時空の回転に対する保存量」が意味するところは、ヌース的解釈からすると、結局のところ、時空の回転に対する観察力ということになります。ここで言っている「時空の回転」がローレンツ変換であることは言うまでもありません。
●結論
水素原子とは外在世界(モノと時空)の認識を形作っている概念のカタチ。すなわち、思形。
Φさんの物理数学的分析と齟齬をきたすところがあれば、ご意見下さい。







7月 14 2008
時間と別れるための50の方法(19)
●4次元と垂子
さて、ここで思い出して欲しいのが、前々回紹介したシリウスファイルの内容です。
「モノから広がっている3次元の方向性はシリウスでは何と呼ぶのですか?」
「垂子(スイシ)です。垂子とは線です。」
僕自身、この情報を受け取ったばかりの頃は、OCOTが何を伝えたいのか皆目、見当もつきませんでした。しかし、あれこれと考え続けるうちに、この「垂子(スイシ)」という概念が4次元方向の軸そのもののことを語っているのではないか、という見当がついてきました。「スイシ」という言葉は単に音声で伝えてられてきたものだったのですが、この言葉に「3次元に”垂”直に交わる観察子」という意味で「垂子」という漢字を当てたのも、「スイシ」が僕らにとっての4次元の方向を意味する概念ではないかと直感したからです。
どうやら4次元の方向の「軸」は、僕らの空間認識ではモノから広がる3次元の「球空間」そのものとして入り込んできている………このように考え出すと、今までお話してきた、ψ3とψ4という互いに反転した3次元の球空間が4次元世界を構成するための第4の軸と深い関係を持っているのではないかということが予想されてきます。そこで、このイメージをより強固なものとしていくために、ψ3~ψ4が形作る3次元の二つの球空間の関係を、他者側からのψ*3〜ψ*4も考慮した上で、次元を一つ落とした形で比喩的に表して見ることにします(下図1参照)。
この図1では例によって3次元空間が平面で表されています。4次元方向の軸はこの平面に直交する一本の線として表わすことができますが、このとき、ψ3〜ψ*3が形作る3次元の球空間は原点0で互いに接する二つの小さな3次元球面P、P*として描かれています。球面P、P*はともに4次元方向の半径 i t(- i t)がゼロにまで潰されたものなので、原点0そのものと言い換えてもいいのですが、ここには相互反転関係における外面と外面*という差異が存在しているわけですから、その4次元球体の半径が無限小の長さを持つという意味でΔw、−Δwとして示しています。これらψ3〜ψ*3の方では3次元空間が球面上に丸められともに無限遠方が一点∞と∞*で同一視されているのが分ります。当然のことながら、相互反転した3次元空間上の無限遠を意味するこの2点は4次元軸上にあります。
一方、ψ4〜ψ*4それぞれの球空間は二つのラッパ帽のような曲面(3次元双曲面)として表されています。この形は以下のような数学からの要請です。
x^2+y^2+z^2+w^2=1………これは3次元球面の方程式です
x^2+y^2+z^2−w^2=1………これは3次元双曲面の方程式です
この双曲面を広げていく4次元方向の軸は図にある通り時間tに対応しており、自他における時間の方向は同じですからここではともにtにしています(時間の符号が自他側で変わらないというところが時空がψ4とψ*4の同一化によって生まれているということの意味でもあります)。
このように4次元軸上には軸自体の反転によって、3次元空間を相異なる2種類のカタチで表す方向性が存在しているわけです。ヌース理論ではψ3〜ψ*3を人間の外面のカタチ、ψ4〜ψ*4側が人間の内面のカタチとして考えます。
このことは『人神/アドバンスト・エディション』でも触れたように、人間の外面のカタチが人間の内面のカタチである時空(3次元双曲面)上の一点に小さく丸められて貼付けられていることを意味します。以前この論考で「ψ3は一体どこに行ったのか?」という問いかけをしましたが、この問いかけの答えはここにあります。つまり、人間の外面は時空上のあらゆる原点の中に3次元球面状のモナド(精神=無意識)として映り込んでいるのです。この映り込みが物理学が素粒子の場として記述している内部空間と呼ばれているものとやがて深い関係を持ってくることになります。一言で言えば、内部空間とは無意識化した人間の外面の場の構造体であるということです。このような考え方をもとにして「素粒子空間=人間の無意識構造の場」というヌース理論の重要かつ特異な主張が展開していくことになるわけです。
さて、話を4次元の軸に戻しましょう。上に挙げた図1から、4次元方向の軸は3次元の球空間全体を傘を閉じたときのように一本の線の中に凝縮させている様子がうかがえます。ψ3側とψ4側の違いは、ψ3側が3次元空間の無限遠方を一点で同一視して3次元球面のカタチを半分だけ(多様体としての3次元球面にはまだ成り得てないということ)なぞっているのに対し、ψ4側の方は、3次元空間がそのまま無限に広がって開きっぱなしの状態になっているということが分ります(同様にψ4も多様体としての4次元時空には成り得ていません)。ψ4側で3次元空間が開いてしまった原因は、モノの手前側に自分の顔を想定してまったことです。この想定がなければ視野にはただ無限の深さを持った空間が存在するだけであり、その深みには視野自体を開示させている無時間としての光が存在するだけです。そして、この光の場においては3次元の球空間は一本の線分として見なされなければなりません。これは別の言い方をすれば「この領域に入ったならば今まで球面と見ていたものを点と見なせ」ということです。
球面概念を点概念へと変換する——ヌース理論ではこうした概念操作を「面点変換」と呼びます。次元観察子が上位の観察子へと次元上昇を果たすとき、必ずこの面点変換が起こると考えて下さい。たとえば、ψ1〜ψ2の球空間(モノ)からψ3〜ψ4の球空間(モノの周りの3次元空間)へジャンプしたときのことを思い出してみて下さい。あのとき、モノは回っても背景空間は回っていないという知覚的事実を皆さんは発見したはずです。これは面点変換の考え方を使えば、モノとしての球体がψ3〜ψ4の球空間上では一方向の線分の意味しか持っていないということを意味しているからです。つまり、一個のモノに対する観察の視線はモノのあらゆる見えの空間(ヌースでは表相といいます)を含み持つものとなっていますよ、というわけです。これと同様なことがψ3〜ψ4レベルにおいても起こるのだと考えればいいでしょう。その意味で言えば、ここで起こる第二の面点変換は次の観察子レベルであるψ5〜ψ6領域へとジャンプするための幾何学的な手続きのようなものになっています。この手続きはとても重要です。なぜなら、面点変換によって3次元の球空間を線と見なしたときに、僕らは始めて4次元空間における線の意味に触れることができるからです。3次元空間での線の描像を引きずったままでは4次元は4次元時空としてしか現れることはなく、4次元空間は決して見えてこないのです。
あなたがたが今持っている3次元認識からこの4次元認識への移行は同じ1次元の差であっても、2次元から3次元へ移るのとはかなり大きな違いがあります(『人類が神を見る日/アドバンスト・エディション』第1部p.86)
——つづく
By kohsen • 時間と別れるための50の方法 • 0 • Tags: モナド, 人類が神を見る日, 内面と外面, 無限遠, 素粒子, 表相