2月 1 2008
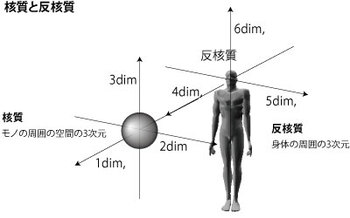
核質と反核質
今回の本ではヌース用語の乱発は極力避けた。これも今までの反省から。概念が十分に醸造されないままヌース用語を多用してしまうと、大方の場合、呪文にしか聞こえず、理解の妨げになるからだ。
今回のアドバンス・エディションを読んでもらうと分るんだけど、ヌース理論が試みているのは空間に潜んでいる高次元の次元階層を見抜く知覚能力の獲得なんだよね。空間を単なる3次元(時間を含めれば4次元)と見なしているのが僕らの通常の感覚なので、その意味で言えば、ヌースは超感覚的知覚(ESP)の奪取を目論んでいると言えないこともない。こういう言い方をするとさも難しい話のように聞こえるかもしれないけど、何のことたあない、ヘイ、エブリバディ、物質的な空間からゲットアウトして、身体的な空間にゴーしようぜ、と言ってるだけなのだ。ん?なんで今日はルー・大柴なんだ?
現在、執筆中の『The NOOS(仮題)』では、この身体を巡る3次元性を中心に心理学、物理学、神話、歴史、芸術、哲学、細胞、大気圏、地球、月などスキゾフレニアックに話がいろいろな横断を見せながら進んで行く。今回のアドバンス・エディションはこの新著へスムースに入れるようにするためのとりあえずのウォーミングアップと思ってもらうといいかなぁ。この100ページほどの付け足しは一言で言えば「身体における前-後とは何か」について書いている。
「前-後」と言っても物質的身体のことじゃないよ。意識的身体としての前-後ね。ここには実は鏡の秘密が潜んでいる。いきなり神道チックな表現を使えば、ヤタノカガミという迷宮から出るための最初の謎解きが、この前後のなぞときにあるってことだね。人間を構成している霊的な構造にはこうした鏡のペアが全部で4組存在させられていて、それら4組の合わせ鏡の秘密を順番に解いていくことが、ヌースがいう「次元観察子の顕在化」のことなんだ。カガミの秘密をすべて見抜いてしまえば、その中に閉じ込められていた黒いカラスはフェニックスへと生まれ変われる。フェニックスが生息している領域は空間次元でいうと7次元世界だな。仕組みはカンタン。
1、2、3
4、5、6、
7、8、9………
というように、空間の次元はあたかもマージャンパイのごとく構成されていると思えばいい。要は1次元の上には4次元が、4次元の上には7次元が常に同居してますよ、ってことだ。つまり、次元はイッスーチーの三面待ちをやってるのだ。ろ〜ん。
1、2、3次元とは、言うなれば物理学が用いているx-y-z、つまりモノを存在させている空間の3次元性だね。そこに身体における「前」が第4の次元として入り込んでくる(ここからヌース独自の空間論に入ってくる)。モノへの現実的観察が行なわれている空間だ。現実的観察はつねに「前」でしか行なわれることはないので、じゃあ「後ろ」って何だ?ってことになってくる。今度の本の第二部ではそんなことを100ページも費やしてシコシコ書いている。
そんなかんだで、大雑把、フランク・ザッパに言ってしまえば、身体の周囲に感じている3次元は実は、4、5、6次元になっているってことなんだ。巷で次元上昇、次元上昇って騒がれているけど、何のこたーない。人間自身の実存的な場所を再構築するってことがヌース的には次元上昇の本質なわけだ。ヌースではモノが存在する空間の3次元性のことを核質(かくしつ)って呼ぶ。ほんでもって、人間の身体が存在している3次元性のことを反核質って呼ぶ。核質は3次元空間で反核質は6次元空間。そしてそれらの対称性を見出すことを「核質の等化」といい、そこに観察精神ってやつが介入してくる。
実際、街に出たら分るけど、そこにはたくさんモノや人が忙しく動き回っているでしょ。つまり、空間には3次元と6次元が重なっているわけだ。で、その様子をまた君は「前」で見ることができている。。これは、ある意味、核質と反核質が7次元によって等化されてしまっているからなんだけど、その反映として中和側に位置させられた人間の意識にはその次元的な重なりに全く気づかないんだな。
そこまでの次元上昇の仕組みがぜぇ〜んぶ見えるようになることをヌースでは「覚醒」といいます。
2013年から空間に潜在化しているこの次元の差異の序列がぜぇ〜んぶ見えてくるようになります。というか、ヌースがぜぇ〜んぶお見せします。7次元が見えてくると、ようやくそこに宇宙空間との接続ができてきて、太陽系空間=原子空間への扉が開いてきます。。。。ほんとか?ほんとです。乞うご期待。







2月 6 2008
ヌースアカデメイアの半田です。
最初は4~5分ぐらいの簡単な「こんにちは/よろしく/じゃあまたね」的ビデオにしようと思っていたのだが、話しているうちに、何か話がいつものレチャー風に。。あわわ、いかん、いかん。難しい話は初っぱなは禁物。横道に逸れるなよ、こうせんくん。ありゃま。気がついたら15分以上話してました(^^)。
それにしても、オーディエンスがいないところでのモノローグはやりにくいなぁ。人間はやっぱ他者がおらんといかんね。あんなこんなで15分の丈になったものだから、結局、締めが必要になっちまった。。。で、ニューヌースアカデメイアのマニフェストを朗読することに。。あ〜、こんなことなら練習しておけばよかった。。。
ってなことで、ビデオメッセージ、見てやって下さい。
→半田広宣ビデオメッセージ001
(※ビデオメッセージをご覧頂くにはQuickTimePlayerが必要です。)
サイトの方からは日本語フロントページの「profile」をクリックすると入れます。
僕としてはこちら側から入って、BGサウンドをそのまま流しながら見てくれるとうれしいかな。。
話のリズムのなさをビートが補ってくれてるからね(^^
By kohsen • 10_その他 • 6