9月 30 2008
時間と別れるための50の方法(39)
●知覚球体と4次元軸
(38)からのつづき——前回の最後に「知覚球体が次元観察子ψ5」という旨のことを書いてしまいましたが、記憶力のいい方は「あれ?ちょっと前の説明と違うんじゃない」と思われたかもしれません。そうです。第34回の図1における説明では、観測者における3軸回転の綜合(数学の言葉では3次元回転群/S0(3))を次元観察子ψ5のカタチとしています。しかし、知覚球体を包んでいる知覚球面は(これは2次元球面ですからS^2で表しましょう)は身体の左右方向(これをx軸としましょう)と上下方向(これをy軸としましょう)の2軸による回転によって作り出すことができます。ということは、ψ5としての正確なカタチである観測者のSO(3)を作り出すためにはz軸、つまり前後方向そのものを軸とした回転を加味する必要性が出てきます。この回転は視線回りの回転ですから知覚正面自体の回転の意味を持つことになります。ちょっと実際には作り出しにくいですが、首を傾げるときに生まれている回転の方向のことですね。その意味で、ψ5の正確なカタチは下図1に示すように「知覚球面を知覚したときにおける、そのときどきの視線を軸とした回転の綜合」といえます。
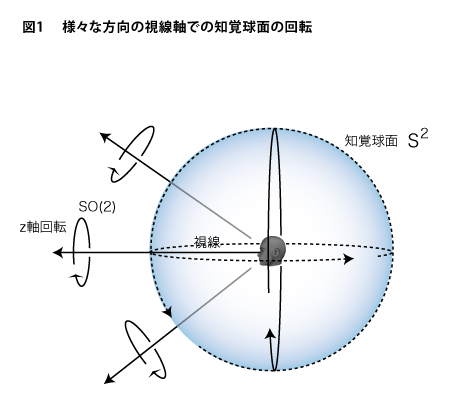
このカタチの描写はダイレクトには図示できないので、比喩的な言い方になりますが、知覚球面上のあらゆる点に槍が突き刺さって、その一点一点上でグルグルと渦が起こっているような状況です。数学では3次元回転群SO(3)は2次元回転群SO(2)と2次元球面S^2の積として表すことができます。
SO(3)=S^2×SO(2)
では、このような観測者自身の回転の綜合は3次元球面S^3に対してどのような運動として現れてくるのでしょうか。以前、次元観察子ψ3~ψ4の説明のところで、視線は4次元方向の線分ではないのかという予測を立てました。あのときは、観測者が一つのモノの周囲を回ったところに綜合化されている球空間の半径部分は、結局、どの半径を取ろうとも「身体の前」であるがゆえに、この「身体の前」を不動な方向と考えて、視線自体を4次元の方向と見なしてよいのではないかと推論しました。
この次元観察子ψ5のレベルでも全く同じことが起こっているのが分ります。観測者がその場でいくらグルグルと自転しようとも、そこに現れる風景は身体側を基準として見ればやはり「前」という名の一方向にすぎません。僕らはついつい「前」が回っているという表現を取りがちですが、実際には「前」は顔面が向いている方向を指す言葉なわけですから、知覚球面自体も身体を基準とした空間から見れば「面」ではなく、「常に前という一方向に存在する」という意味で「点」と見なす必要が出てきます。つまり、ここでも例の「面点変換」の考え方が生きてくるわけです。そうすると、このとき、知覚球体自体はそれこそ「世界に対する観測者の不動の視線」という意味で、4次元方向に引かれた線分の意味を持つことになります。つまり4次元の方向を描像するためには従来の球体認識を線認識に変える必要があるということです。
ということは、上に書いた「知覚球面を知覚したときにおける、そのときどきの視線軸に対する回転」とは、結局のところ、4次元方向を軸に持つ回転が3次元認識においてバラバラにされて現れてきた状態ではないのかと考えることができます(あくまでも推理です。数学的な証明は分りません)。前回の解説における図3を用いてこの視線軸に対する回転の綜合の様子を表せば、今度は3次元球面そのものに4次元方向を軸とした回転Eが与えられているイメージが作り出されてきます(下図2参照)。つまり、4次元軸での3次元球面の回転というのは、知覚球面上の様々な方向へ放たれた視線回りの回転を一つの回転に置換する意味を持っているのではないかということです。そして、これはいい換えれば、身体における絶対的前方向を軸とする回転だともいえます。
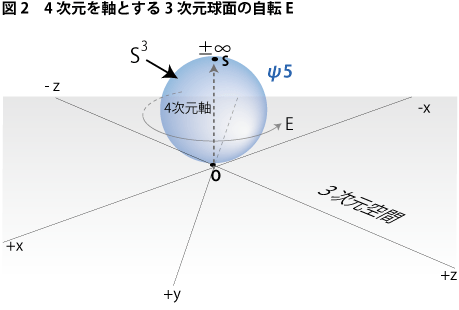
「わたし」がどのように動こうとも決して動くことのない「前」。車が走行している様子であれ、飛行機が航行している様子であれ、太陽が運行している様子であれ、そして、たとえ「わたし」が歩行している様子であれ、例の眉間鉛筆よろしく、すべての運動はこの視野空間という「不動の前」において認識されるしかないのです。ということは、この「不動の前」とは4次元空間上の3次元球面の自転軸に対応させることが可能になってきます。言い換えれば、この軸は主観が視覚として経験できる全空間を幾何学に綜合したものとなっているわけです。
次元観察子ψ5。3次元球面とその自転軸。それはヌーソロジーでは自己の場を規定する観察子として定義されます。これは「わたし」が視覚的に触れることのできる全空間のカタチを意味しているということです。そして言うまでもなく、この軸もまた奥行きが一点同一視されていますから、人間の内面認識にとっては長さが無限小にまで縮められた超ミクロの世界に存在していることになります。——つづく







10月 6 2008
時間と別れるための50の方法(40)
●ψ5の反映としての次元観察子ψ6(丸められた時空と開いた時空)
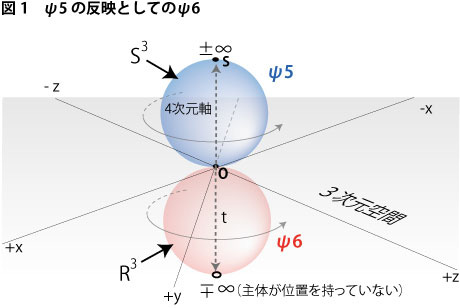
では、今度はこの4次元のアナロジー図を使って次元観察子ψ6のカタチがどのように表されるかを見てみましょう。下図1をご覧になりながら以下の解説を読んでみて下さい。
次元観察子ψ5がψ3とψ4の等化作用として生じる観察子であるのに対して、ψ6の方はその反映としての中和作用の次元になります。中和ですから、ψ6においてはψ3とψ4の対称性が形作られはするものの、その内実はψ5の様子とはだいぶ違ってきます。まず言えるのはψ5では無限遠点が主体の位置として自覚されているのに対し、ψ6にはそれが全く見えていないということです。その理由はおおよそ次のようなロジックで説明することができます。
まず、ψ5は人間の外面であるψ3を先手にして後手のψ4との関係を等化に持っていきます。この働きを空間の掛け算で表し、
ψ5=ψ3×ψ4
としましょう。これは前回説明したように、3次元球面が表裏で二重化する意味を表したものです。
一方、ψ6の方は人間の内面側であるψ4を先手にψ3との等化をはかろうとします。これは掛け算の順序を入れ替えて、
ψ6=ψ4×ψ3
で表すことができると考えましょう。
通常の掛け算であれば、A×B=B×Aとなり交換法則が成り立つのですが、観察子同士の掛け算は演算子の積と同じで、ψ3×ψ4とψ4×ψ3ではその結果が全く違う形を提供してきます。
人間の外面であるψ3の方は無限遠点に主体の位置が収まったカタチでした。ですから、3次元空間は3次元球面のカタチとして現れます。そこでψ3は、自身の反映としてのψ4を自分自身の反転したものとして見るのですが、当然、ψ4が自身の反転した映し絵であるならば、ψ3はψ4側の無限遠点にも主体位置があることを知っていることになります。それによって、等化によってψ5の形成へ進もうとするときに、反転した3次元空間側の無限遠点にも主体の位置を当てはめてくるというわけです。こうしてψ3の無限遠点-∞とψ4の無限遠点+∞はψ5において重合し、±∞として主体位置である点Sを完全化させることになります。
一方、ψ6=ψ4×ψ3の方では全く逆のことが起こるのが分ります。ψ4側では精神が働いていないので、無限遠点+∞が主体の位置であるという認識は生まれてはいません。ですから、ψ6がψ5の反映の作用であるψ4×ψ3としてψ4とψ3との間で対称性を取らされようとするときに、ψ6はψ3の無限遠点-∞に主体の位置があるということを見逃してしまい、結局、3次元空間をコンパクト化する(丸めるということ)ことができずに、そのまま3次元空間を開かせた形で二重化した3次元空間(多様体)として出現してくることになります。図1に示したψ6の球面の無限遠点が白い穴で表されているのが3次元が球面として閉じていないということを表しています。これがいわゆる多様体としての3次元ユークリッド空間です。
それに加えて、この3次元ユークリッド空間にはψ5が作り出した4次元の回転軸が反映として入り込んでくることになります。この反映はψ6においては4次元軸の方向の反転として現れ、4次元の計量の符号を正から負へと逆転させることになります。以前も説明したように、これが物理学が時間tとして扱っている次元に当たります。この結果、次元観察子ψ6は僕らが時空(局所)と呼んでいるものとして現れてくるという仕組みになっているわけです。
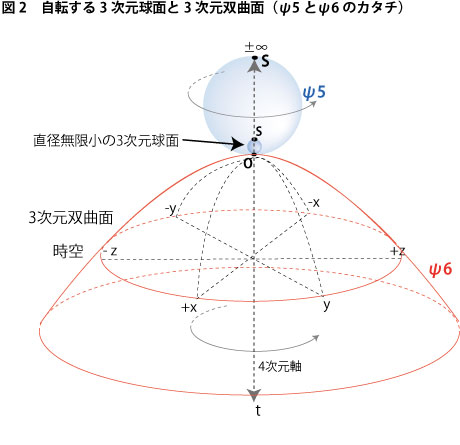
図1ではψ5とψ6の対性を強調するためにψ6も球面状のカタチで表してしまいましたが、こうした開いた3次元空間に時間が加味された時空のカタチは数学的には3次元双曲面として表されます。そのカタチを使って図1を書き直すと、次元観察子ψ5とψ6の幾何学的関係は下図2のように表すことができます。
次元観察子ψ5=3次元球面の自転とその自転軸
次元観察子ψ6=3次元双曲面の自転とその自転軸
この図の意味を簡単な言葉で表すと、(34)の図1で図示した観察者における前方向が作るSO(3)と後方向が作るSO(3)のそれぞれの空間のかたちの関係と言えるでしょう。実際に物理学では、時空R(1,3)のかたちは、
R^1(+)×SO(3)
とされています。後ろは視覚(光)が生み出されていないという意味で無限遠に主体の位置を置くことができず、文字通りどこまで行ってもたどり着けない場所として永遠に開いています。その意味で、時空は後ろ方向であるR^1(+)という半直線に3次元回転群SO(3)を作用させたもので表すことができるということです。
このψ5とψ6の関係性をさらに正確に描写するためには、例の「前方向は一点同一視によって長さが無限小にまで縮められている」という知覚的事実を盛り込む必要性が出てきます。結果、次元観察子ψ5は時空における原点Oに小さく小さく張り付けられた3次元球面の自転とその自転軸として密やかに活動していることになります(図2参照)。こうして次のような推論が導き出されてきます。
観測者に実際見えている前の世界は実のところ無限小の大きさにまで小さく小さく縮められて、後ろが作り出している広大な空間の中にすっぽりと収まってしまっているのではないか――前は持続を伴った主体(いつでも今、どこでもここ)として働き、後はそれらを時系列に沿って断片化させた瞬間時刻tと瞬間位置(x,y,z)の概念として働いているのではないか。。何という皮肉。見えている世界(前)が実は精神で、見えていない世界(後)が延長=物質となっているのだ。人間の認識はここにおいても転倒を余儀なくされている。。
さて、ψ5~ψ6のここまでの解説で、これらの幾何学的構造が訴えている意味は何なのでしょう。少し想像力を使えばそれはおのずと分ってきます。つまり、こういうことです。本来、世界には見ているものも見られているものも存在しておらず、世界自体はその起源として一つの存在であるということです。そして、世界は世界を見るものと見られるものに分離させるために、つまり、世界が世界を見ることを欲したために、3次元空間を閉ざして球面化させる方向と、そのまま開かせて時空を生み出す方向を作り出した、ということになります。
主体が客体として錯覚されている世界。それが人間なのです。
――つづく
By kohsen • 時間と別れるための50の方法 • 2 • Tags: ユークリッド, 内面と外面, 無限遠