トランスフォーマー型ゲシュタルト

●メビウスの帯とスピノール………（2）
　前回からのつづき——まず、リボンを用意し、その両端ををリング状につなげます。リボンの中央上に任意の1点Sをとり、その外面側と内面側をそれぞれ点s、点s*とします。ここで外面側であるs点と内面側であるs*点を左の親指と人差し指で軽くつまみます。この「つまみ」は、点Sがこのリボンの内面と外面の両面にある点sと点s*による挟み込みによって与えられているということを意味します。ここで、リングに沿って二本の指を点Oを中心に回転するように滑らしていきます。180度滑らしていくと、スタート地点の反対側にまできますが、そこで二本の指を見ると、相変わらず外面側に親指、内面側に人差し指が添えられているのが分ります（下図1）。まぁ、当たり前の話ですが、これが通常の3次元空間での回転の性質です。

　次にスピノール空間の場合を考えてみます。スピノールの回転する空間ではスタート地点と回転中心Oを挟んだ反対側の位置では外面と内面の関係が互いに捻れ、S（＋∞、－∞）がS*（－∞、＋∞）となっていました。3次元空間では無限遠点と云えども4次元空間上ではただの点にすぎませんから、＋∞、−∞二つの無限遠点をそれぞれs、s*と置いてみましょう。すると4次元空間においては、点S（s、s*）を指し示しているスピールが半回転する間に、このリング自体がちょうど180度の捻れを作り、点S*（s、s*）を指しているということになります。そして、元の位置に戻ってくるまでにもう180度の捻れを作っており、早い話が、スピノールが回転によって次々と指し示して行く円環の位置はスピノールが一回転する間に360度の捻れを持っているわけですです。このことからスピノールの一回転が描く軌跡は二回捻りを入れたメビウスの帯と同じ形をしているということになります（下図2）。
　

　
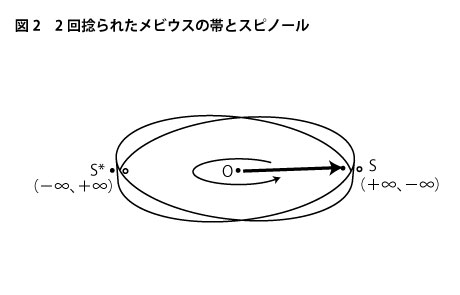
　前回の図2で示したように、通常のメビウスの帯の場合は一回しか捩じれていないので、一回転回ってきたときに、表裏の関係が入れ替わりますが、二回捻れでは、半回転でそれが達成されるわけです。ということは、通常のメビウスの帯を2回巡ってくることと二回捻ったメビウスの帯を一回巡ることは、全く同じ意味合いを持っていることが分かります。つまり、1回捻れのメビウスの帯状の720度回転が2回捻れのメビウスの帯状の360度回転に対応しているわけです。通常の空間の回転角度をθとすれば、スピノールの空間の回転はθ/2でθを実現させます。
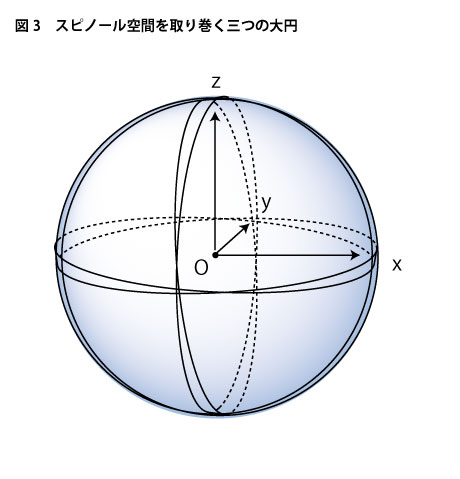
　このような描像を持つことによってスピノールが張られた球空間の形がそれなりに輪郭を持ってきます。つまり、このスピノールが活動している球空間においては、このような円環構造が下図3のようにx、y、zの3方向すべてにおいて成り立っているわけです。はてはて、これは一体どんな形なのでしょう。
　

　
　ここまでスピノールの回転の描像について見てきました。ヌーソロジーで見れば、4次元空間上でS（＋∞、－∞）とS*（－∞、＋∞）として対峙し合うのはψ5とψ6、つまり自己と他者の位置です。ここで『人神/アドバンストエディション』にも登場した「背中合わせの自己と他者」という関係を思い出してみて下さい。それらは同じ無限遠点±∞で背中同士でくっつき合っていました。つまり同じ位置にいるのです。ただ、自他では互いに向いてる方向が逆なので、前後方向が相互に逆になっています。つまり、点SとS*は同じ位置とも言ってよいのですが、冒頭に挙げた親指と人差し指の鋏み込みのように、一点を表裏の2点で指定しているために、その表裏の方向性の在り方によって二通りの組み合わせが出てきてしまうのです。このことは、図2に示したスピノールの回転が作り出す円環における二つの極点SとS*の位置も実は互いに重なり合って繋がっているということを意味しています（図ではそうは見えませんが繋がっていると考えて下さい）。つまり、回転中心Ｏ点からS点までを結んでできるスピノールはそのまま反対の極のS*点につながり、S*点からまた中心のＯ点に戻ってくるような円構造を持っているということです。このスピノールの回転が作る円の内部と外部をもし反転させて見ることができれば、二つのスピノールが一点を挟み込むようにして指定している様子が伺えることでしょう。
　ということは、結局のところ、スピノールが張られている空間のかたちは3次元球面S^3の形状そのものということになります。物理学ではスピノールが張られる球空間での3次元回転は複素2次元回転群SU(2)として表されるのですが、実際、このSU(2)の形は3次元球面S^3と同じものとされています。

　さて、さて、スピノールが回転している球空間の構造の方はかなりはっきりしてきたのではないかと思います。問題はこの構造が一体何を意味しているのかということです。僕らが何気に暮らしているこの空間の極微領域には現実としてこのような球空間が存在していることを物理学は実証しています。自然は一体なぜ、時空の根底にこのような超ミクロの3次元球面の構造をセットしたのでしょうか。この空間が一体どのような意味を持つ空間なのか、これからヌーソロジーの思考方法で探っていくことにしましょう。ここから、いよいよヌーソロジーが描く異次元世界への旅へと本格的に入っていくことになります。それはトランスフォーマー型ゲシュタルトによる新しい世界観の幕開けとも言っていいものになるでしょう。あっと驚く空間風景が展開してきますよ。お楽しみに。

●4次元知覚の世界へ（脱-表象化の世界へ）
　さて、「時間と別れるための50の方法」と銘打って『人神/アドバンストエディション』で補填した小論『トランスフォーマー型ゲシュタルト――ベーシックプログラム』の内容のより噛み砕いた解説を試みてきましたが、この次元観察子ψ5～ψ6レベルの説明の段階に至って「4次元空間の方向が観測者の絶対的前そのもののことである」という内容にかなり戸惑っていらっしゃる方も多いのではないかと思います。かくゆう僕もこの結論に達するまでかなりの紆余曲折がありました。

　約10年前に例の「立方体鉛筆」（『人神/アドバンンストエディション』p.179）でその位置に接近遭遇したものの、そこから4次元の論理をどう組み立てていいものか見当もつかず、シリウスファイルはもちろんのこと、哲学書や慣れない物理書や数学書と睨めっこする日々が続きました。「前が4次元空間の方向である」とする言説が思考として力を持つためには、もしそのように世界を見たときに、一体、どのような新しい知識が僕らにもたらされるのか、さらには、そこで獲得された知識によって、これまでの世界がどのような意味の変更を迫られるのか、その具体的なビジョンが得られる必要があります。つまり4次元から見た知の体系、概念の体系の素描が求められてくるわけです。そのビジョンが構築できる可能性がなければ、この言説は、巷に氾濫している「霊界とは4次元である」といったようなトンデモ言説と何も変わるものではなくなってしまいます。

　4次元世界に関する考察は『光の箱舟』にも書いたように、百年以上も前からたくさんの思想家、哲学者、科学者によって為されています。しかし、未だにその正体は解明されてはいません。もちろん、4次元なんてものは所詮、人間の想像力の産物であって、理性自体が3次元認識をベースとして構造化されているのだから、理性によって4次元を捉えることなど不可能だ、と考えることもできます。しかし、時代は今や高次元の知覚を要求しつつあります。というのも、物質という存在をそれこそ信念体系としていた物理学自体が、物質の大本の成り立ちに4次元空間は言うに及ばず、それ以上の高次の空間の構造体が暗躍していることを明らかにしてきているからです。

　物質を確かな存在だと認めるならば、当然、そのもととなる高次元空間も確固たる存在だと言わざるを得なくなります。しかし、物質という概念に捕われている思考（人間型ゲシュタルト）には、それらの高次元がいかなる意味を持っているのかについては皆目、見当もついていないというのが現在の思想状況です――このように、4次元以上の高次元空間とはいわば人間の宇宙に対する理解を阻んでいる強固な障壁となっているわけです。わたしたちが近代以降培ってきた思考の道具ではおそらくこの障壁の乗り越えは不可能でしょう。4次元空間とは何かという問いに対する回答には、当然、この壁を乗り越えられるだけの力がなくてはなりません。上にも書いたように、世界を別の風景へと変貌させる意味の連結、連動、連鎖が存在しなければならないのです。
　さて、もう一度いいましょう――4次元空間の方向とは観測者の絶対的前そのもののことである。
　果たしてここからいかなる新しい世界の展望が開けてくるというのでしょうか。今まで書いてきたことを念頭において、ヌーソロジーが4次元空間を考察していくに当たっての前提とする内容を箇条書きにまとめてみましょう。

1. 4次元空間を通常の意味で「知覚する」ことは不可能である
2. 4次元空間は知覚対象というよりも、知覚そのものが持っている空間的機構と深く関係している
3. その意味で4次元知覚というものがあるとすれば、それは知覚の機構自体を知覚するメタ知覚といえる
4. よって、4次元知覚においては従来の表象（触覚、視覚、聴覚等によるイメージ物）は一切存在していない
5. 4次元空間は光速度状態において見える空間である（奥行きを同一視するということ）
6. よって、4次元空間においては従来の時間概念は意味を持たない（光速度では時計は止まるということ）
7. 4次元空間における一つの方向、つまり、線には主体という概念が配置されている
8. この線には長さという3次元的な尺度は存在しない（∞=1/∞という対称性が成立している）
9. 4次元空間上に引かれた複数の線はおそらく「比」という関係だけを持つ
10. その意味で、4次元空間とは真の形相（カタチ）が存在する場所だと考えられる
11. ここでいう真の形相（カタチ）とは物質を創造していくための思考物体のことである
12. この思考物体がヌース（旋回的知性）が知覚対象とするイデアである

　この諸前提に留意しながら、もし4次元知覚の獲得に成功した知性があるとすれば、自己や他者、さらにはモノといった普段、接し慣れている諸事物が一体どのように見えてくるのか、もう少し具体的な描写を試みていくことにします。そこに予期しなかった意味の連結や連動が起こってくるならば、それこそ「ガッチャ!!（Gotcha!!）」です。——つづく