5月 5 2009
『ラス・メニーナス(侍女たち)』――人間型ゲシュタルトの起源、その6
3、第三の軸――階段の男、もしくは上と下
さて、次に「階段に立つ男」についてフーコーがどう書いているか見てみよう。
彼がどこからきたのかはわからない。はっきりしない回廊づたいに、人々が集まり画家が仕事をつづけているこの部屋のまわりをまわってきたと想像することもできるだろう。あるいは彼自身、ついさっきまで、場面の前面、絵の中のあらゆる目が凝視している不可視の領域にいたのかもしれない。鏡の奥に認められる像とおなじように、彼も自明であるとともに隠されている、あの空間からひそかに使わされた使者かもしれぬ。といっても相違がないわけではない。彼はそこで生身の人間であり、表象されている区域の境界に外から姿をあらわしたところだ。彼はまぎれもない存在にほかならない。(M・フーコー『言葉と物』p.35)
階段の男からは画家の描く王の姿と実際の王の姿が見えていることだろう。そしてまた、彼の視野の中には画家の後ろ姿が確実に捉えられている。フーコーがいうように、もしこの男がこの部屋の中をついさっきまで徘徊していたとれば、壁に掛けられている小さな鏡の存在も知っているだろうし、その鏡に王が映り込んでいることも周知のことだろう。さらに言えば、この部屋にいるあらゆる人物と会話を交えながら、彼らの視座に近づいては王と画家の噂話を彼らの耳元で囁いていたかもしれない。となれば、このどこからきたのか素性がわからない男は、右の窓から差し込んでこの部屋を満たしている光の全体性を自らの眼差しの中に溶かし込んだ存在の象徴化とも言える。しかし、その眼差しはその光と同一のものというわけでもない。なぜなら、今、現在の彼の視線は右手に穿たれた窓の方からではなく画家の後上部にある階段奥の回廊から差し込んでくる光に沿うようにしてこの部屋に入射してきており、彼が立っている場所も部屋の中の諸人物たちよりも幾分高みの位置にあるからだ。そして、何より、この男を部屋の外部にまさに出て行かんとする存在として認知できているのは、この構図の中ではただ王(と王妃)のみである。
前回、左右方向からの視線は超越的なものだと語った。〈前-後〉と〈左-右〉が直交関係にある限り、この両者、つまり、〈わたし/あなた〉間を結ぶ視線とこの超越的な視線は互い重なり合うことは決してない。〈前-後〉は常に想像界のうちにとどまり、〈わたし/あなた〉という鏡像を巡って持ちつ持たれつの関係でだた主観的イメージの中で互いの間の乱反射を繰り返す。そのような意識状態に対して、左-右方向からの視線の入射は常に超越者として振る舞い、ときに審判の神として、ときに調停の神として両者の視線を同一化、均質化させ、第三項的眼差しを持ってこの〈わたし/あなた〉の間に介入する。このことは主観(内在)と客観(超越)が互いに対峙して双方その独立性を保ちながら作用していることを意味しよう。つまり、前-後の観察軸と左-右の観察軸が常時、直交関係を保っている限り、主観は客観を自らのうちに見いだすことはできないし、また、客観側も主観を自分の懐の中に入れることはできない。この作品に即して言えば、そもそも王の主観はそれが主観である限り、客観を形成し得ないし、客観は客観として神の座に座り続けたままで決して王のもとに舞い降りることはないからだ。
こうして意識が次の段階に進むためには「階段の男」の存在が極めて重要な役割を果たしてくるのが分かる——。
彼は部屋を満たす光と同じ視線を持った超越者の化身でもあったこと。
それゆえに彼は王を部屋の中の諸人物の中の一人として一般化させて見ることができているということ。
そして、これが最も重要なポイントでもあるのだが、彼は王によってのみ見られる存在となっているということ。
王から見える「階段の男」………これはまさにこの作品そのものの情景を視野空間の中に納めている王自身の主観の中に客観が入り込もうとしている様子と見なすことができる。主観が客観を自らのうちに内在化させようとしているまさにその瞬間の様子なのである。この「階段の男」の登場によって、超越者として振る舞っていた神の視線は王の眼差しの中に同一化を果たし、王は自らのうちに自分自身を客観視し、自分をみつめる超越者としてのもう一人の自分を自分の心のうちに迎え入れるのである。
この部屋の中で形成されている前後軸と左右軸が作る平面をヌーソロジーの考え方に沿ってとりあえずは5次元平面と比喩的に呼んでみよう。
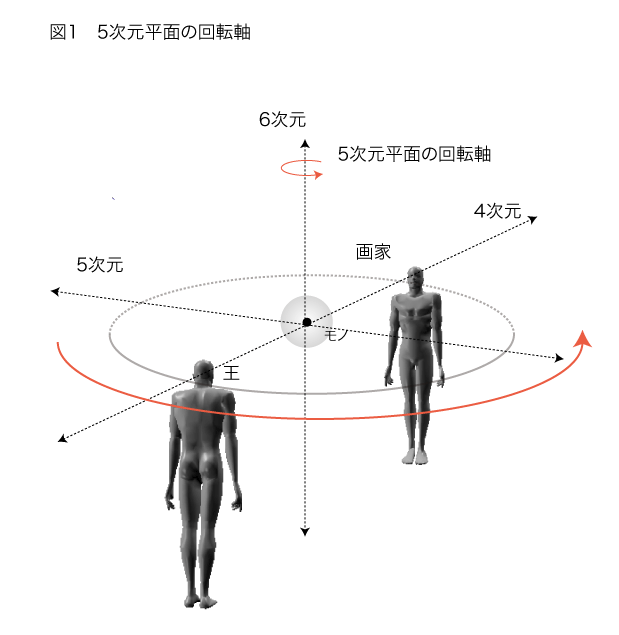
この高次の平面上で一体何が起こっているのだろうか――それはおそらく、王の身体における前後軸と左右軸を交換可能とするような回転が生じているのだ。この回転はそれまで全く対峙的に作用していた神的な視線と主観的視線の区別をなくす働きを持っていると考えられる。当然、その回転を行わせている軸が指し示す方向はこの5次元平面に直交する6次元の方向に向けられており、それはわれわれが普段、何気に上-下と呼んでいる方向ということになるのかもしれない。
全人類にとっての上-下という方向。それは意識平面としての大地を離脱し、地球の丸みを看破した観察の視線の方向とも言えるだろう。その意味で言えば、この絵に描かれた「階段の男」とはこの上-下方向への往来を可能とする観察力を持った6次元空間に座する超越者の姿だということができはしないだろうか。このニュータイプの超越者こそが人間の主観世界に同一化を果たした「我思う、ゆえに我あり」と語る我、すなわちコギトとしての近代的自我の本性なのである。バロック期から古典主義期にかけての時代にヨーロッパの画家たちの無意識は、〈左-右〉方向からの観察軸の成熟から〈上-下〉方向からの観察軸の確立へと向かったのだろう。ここから世界は一気に地動説的世界観へと突入し、地上を俯瞰するこの「階段の男」の視点の登場によって、神の理性のもとに生きていた人々は「理性的人間」という存在に変貌を遂げ、〈前-後〉軸を〈左-右〉軸と全く同等なものとして見ざるを得ない認識へと遷移していったのである。
この新たに設けられた視座が人間に何を招来させたかはもはや言うまでもないだろう。〈前-後〉方向と〈左-右〉方向の差異が全く認識できないのであれば、身体は他の存在物(物質)と同一な空間レベルに堕ちていかざるを得ない。身体空間が本来居住していると思われる4、5、6という空間次元は物質空間が息づく1、2、3次元と何も変わらないものとなり、そこから溢れ出た高次元の差異の力のみが、無意識という正体不明の言葉で呼ばれるようになったということだ。世界は今やこの「人間」が行使する3次元認識の暴力に悲鳴を上げている。無意識は再び目覚めなければならない。7次元からの使者の手によって。
——つづく


 …
…




5月 8 2009
『ラス・メニーナス(侍女たち)』――人間型ゲシュタルトの起源、その7
さて、今までの話からこの『ラス・メニーナス』上において表象化されている観察の視線について再度まとめておこう。
1、身体空間における第一の視線(4次元空間……前と後)
王と画家の視線の関係として表象されている空間の方向性。これは視覚が世界を身体の「前」で捉えるという意味において、身体における前-後方向に築かれている次元でもある。ここには互いの知覚(見る)経験と鏡像(見られる)経験がキアスムをもって構成されており、この方向性だけでは意識は空間の中に明確な奥行き感覚を感じ取ることはできない。
2、身体空間における第二の視線(5次元空間……右と左)
王と画家,互いの視線に対して直交してくる窓からの光として表象されている空間の方向性。左右から差し込んでくるこの光が室内で乱反射を繰り返すことによって部屋全体は明るみのもとに照らし出される。「前」を明るみの世界、「後」を暗がりの世界だとすれば、部屋の中に居合わせているすべての人物たちの〈前-後〉が前後となり得るのはこの明るみが存在しているからである。王は室内にいるすべての人物たちの「前」が集合しているところに自らの視線を遷移させていくことによって、事物の全体性を明るみに引き出し、事物の3次元性を象っていく。この明るみの起源は王にとってはあくまでも左右方向にあり、自らの主観は常にその光が作り出している乱反射の一部でしかない。
3、身体空間における第三の視線(6次元空間……上と下)
「階段の男」の視線として表象されている空間の方向性。この男は窓からの光が充満している室内そのものを他の人物たちとは違った立場から俯瞰できる視座を持っている。この視座は光(客観)を我がものとした理性の象徴と考えていいだろう。彼は王を室内にいる他の人物たちの中の一人としてしか見ていないが、しかし、この男の存在を見ることができているのはただ王のみである。主観(王)はここに超越者を自らの内部に取り入れる事に成功し、超越論的主観性を手に入れる。これが近代自我が持っている統覚の仕組みである。しかし、この統覚は同時に、王自身を多の中の一として一般化する代償として得られるものであることを忘れてはいけない。人間型ゲシュタルトを解体させるためには、われわれは自らの意識を稼動させている無意識を「階段の男」よりもさらに上位に存在する何者かの位置へと進ませなければならない。そうすれば、「階段の男」の登場によって世界から神が駆逐されたように、われわれはコギト=人間を世界から追放できるのだ。7次元空間とはそうした救済者が佇む場所である——ψ13。
ざっと輪郭を辿っただけにすぎないが、以上がヌーソロジーから見た『ラス・メニーナス』のコンポジションに潜在している無意識の構図である。終わり。ちゃん、ちゃん。
何か長くなってしまったなぁ。皆には退屈だったかも。もうしわけないです。次回はここで取り上げた身体空間と宇宙空間の関係についてOCOT情報がどんなことを言ってるか少しだけ紹介してみようかな。。へへ。ぶっ飛んでるよ。予習のため昔のブログにも目を通しておいてね。
予習希望者はこちらへ→『ついでに上と下』 『トツカノツルギ』
By kohsen • 01_ヌーソロジー, ラス・メニーナス • 2 • Tags: ラス・メニーナス, 人間型ゲシュタルト