7月 15 2009
ビートルジュース

ビートルジュースと言ってもティム・バートンが監督したお化け映画の話ではない。オリオン座の赤い星、ベテルギウスについての話だ(ベテルギウス[Betelgeuse]は英語ではビートルジュースと発音する)。先月、ナショナルジオグラフィク誌にこのベテルギウスに起こっている異変についての記事が掲載されたらしい。曰く「この15年間でベテルギウスの大きさが15%ほど収縮している。原因は不明。」ベテルギウスは赤色超巨星と呼ばれるグループに入る巨大恒星である。大きさはちょうど木星軌道と同じぐらいの大きさあると言われていた。それが何とここ15年の間に金星軌道ぐらいの大きさまでに縮んでいるというのだ(15%ほどの縮小にしてはちょっと縮み過ぎ?)。何とも不気味なニュースである。
天体物理の世界では赤色超巨星は質量が太陽の8倍以上もあるような大恒星が辿る次の進化のプロセス段階と見なされている。こうした星は中心部の核融合が鉄まで達するとその反応を停止させ、最終的には超新星爆発を起こすと言われている。で、今回のベテルギウスの突然の収縮騒ぎだが、これはベテルギウス内部の核融合が脆弱化し、今まで核融合のエネルギーによって重力との平衡を保っていた状態が星内部で崩れ出し、重力収縮が始まっている可能性を示唆している。
それにしても15年で15%の縮小とはとても天文学的な数字とは思えない早さである。おまけに研究者の話では収縮速度は年々加速しているという。天体物理の理屈から言えば、その収縮が閾値を超えれば当然のことながらベテルギウスは超新星爆発を起こすことになるのだが、そのときの明るさは最大で満月並みだという。ベテルギウスまでの距離は地球から約600光年ほどしかない。果たして衝撃波等による地球への影響は大丈夫なのだろうか?——というところまでは、あくまでも科学的見地からのお話。
実はこのベテルギウスという星、ヌーソロジーの発祥と極めて深い関係がある。1985年、僕自身、最初の超常体験を経験し、いきなり「オリオンのNOMI」と名乗る意識体からの声が聞こえてきた。その声に導かれるまま、歴史探検やら霊界探検をやらされたのだ。これは神さまのお導きだと信じて疑わなかった哀れな若造は、結果、自分自身の無意識の闇の中に潜むシャドウにボコボコにやられ、見事、発狂。しばらく廃人同様の生活を送っていた。そこで見たこと、そこで聞いたこと、それらは他の日常生活での記憶よりも遥かに鮮明に残っている。ベテルギウスの収縮のニュースを読んだとき、その記憶がはっきりと文字列として甦った。
NOMIはベテルギウスのことを「テツ」と呼んでいた。そして、この「テツ」は現在の人間の霊的な淵源であると言っていた。分かり易く言えば、ベテルギウスという天体は人間存在全体を支えている霊力の反映物だということである。廃人同様の生活を送っていた僕は、当時、冬が到来するだびに、寒空の下、オリオン座の左上隅で赤く輝くこの「テツ」を見つめ続けていた。
OCOT情報には次のようにある。
ベテルギウスとは何ですか?
垂質の等化。
OCOTと交信している当時は「垂質」というシリウス言語の意味をはっきりとつかめていなかったので、当然のことながら、この返答に含まれた意味も分からずじまいだったが、今では朧げながらもある程度の解釈はできる。垂質とは人間の個体を規定する空間のカタチが持った力のことである。ヌーソロジーに詳しい方は次元観察子ψ5のことだと考えてくれればいい。その意味で「垂質の対化」とは自己を規定する空間と他者を規定する空間の関係にある。観察子で言えば、これはψ5とψ*5の関係だ。よって「垂質の等化」とはこれら両者を相等しいものへと持っていこうとする精神の作用を意味することになるのだが、このことは精神分析的に言えば、人間の無意識の欲望を推進させている本源力と解釈できないこともない。つまり、人間の自己における無意識は他者の居所をもとめ、発芽を求め土中を徘徊する植物の茎のように、真の他者との出会いを欲して常時、盲目的な前進を余儀なくさせられているということだ。それは精神分析的に言えば、「他者の欲望を欲望する」欲望として現れる。ヌーソロジーの文脈においては、歴史や経済が見せてきた文明の発展、発達とは、すべてその無意識的欲望の展開の履歴と言い換えてもいい。
他者という存在はヌーソロジーの観点からすれば、真実の自己のことである。人間の自己はこの真実の自己へと辿り着きたいとする本能のもとに、すべての意識作用を営んでいるというわけだ。OCOT情報にいう「垂質の等化」が持ったこのような意味合いは、ベテルギウスが人間存在全体を支えているというNOMIからの情報と極めて近いニュアンスを持っている。
また、次のようなOCOT情報もある。
鉄とは何ですか。
付帯質が持った力の本質。
いつの頃からだろうか。僕はNOMIが語っていた「テツ」とは「鉄」のことでもあると思い始めていた。原子番号26番の鉄はケイブコンパス上で追って行くと、まさに、垂質の等化を行っている精神そのものの位置に当たる。
鉄の減衰——人間という時代を築いてきた自我精神の力が弱まりつつあるのではないか——それがベテルギウスの収縮と何らかの関係を持っているのかもしれない。人間の無意識が真に他者の場所へと辿り着いたとき、すべての価値はニーチェが言うように転換を始めることだろう。否定的な精神の支配は終焉を迎え、肯定的な精神のみの、すべてにおいて「然り!!」と答える全肯定の精神のみの時代が到来することだろう。そのときベテルギウスは赤い星から青い星へと生まれ変わるかもしれない。







7月 23 2009
日食とゾーエー
昨日は日食の日だった。残念ながら博多は曇り空。期待していたようなド派手な天体ショーは見られなかった。
博多では約9割の部分日蝕だったそうだが、曇り空の下、残る一割の太陽光でも地上を照らし出すには十分だった。薄灰色の空の明るみがとりわけ1/10になるということもなく、さほどの大きな変化は見られなかった。しかし、日食が今、現在ここで起こっているという認識のためか、曇り空の下を照らし出している透過光が食の進行とともに微妙に変質していくような不思議な感覚があった。この感覚はなんなのだろう………?光の質感の微妙な変化。そのせいで空間の質感までもが変わっていく。多少の気温変化のせいもあったのかもしれない。大気がそれまでの緊張感を緩め、徐々にぬめっていく感じがした。そのぬめりは決して心地のいいものではなく、かすかな吐き気を伴う感覚だった。
何かに似ていると思った。これはかつてどこかで体験した感覚だ——モスクワだ。モスクワの黄昏。もう20年近くも前になる。所用でロシア(当時はソビエト連邦)に行った。モスクワ入りしたのが夕刻でもあったせいか、やたら空港が暗かった(海外の空港は節電のためかほとんどが照明を落としている)。空港からバスで市街地に向かう途中、道路沿いに整然と並べられたナトリウム灯が共産主義が生み出した味気のない建物群を鈍いオレンジ色の光で照らし出していた。ところどころに掲げられたキリル文字のネオンサイン。日本の都市とは似ても似つかぬ情景。そのときのモスクワは僕にとってまるで異星の植民都市のような雰囲気を醸し出していたのだ。グレーがかったオレンジ色で染め上げられた街並は奇妙な湿度を漂わせ、どこか夢見の空間のようでもあった——。
日食とナトリウム光が具体的にどのような関係にあるのかは分からない。しかし、この二つは確実に何かによって結ばれている感じがする。
* * * *
月が太陽を食らう。この現象に一体どのような意味があるというのだろう。古代人は日食を悪魔の仕業と恐れたという。それは現代人にも分かる自然な感情だ。太陽とは大地に恵みをもたらす豊穣なる生命力の象徴であり、太陽抜きで地上の生命は生きることはできない。
その太陽の営みを月が遮る。それが日食だ。月は何のために太陽の光を遮るのか。月とて生命の母胎として地球上の生物たちに測り知れないほどの影響を与えているではないか。月はなぜ太陽の邪魔をしようとするのか。これは神学的には極めて挑発的な問いかけである。
太陽が持った生命力と月が持った生命力。この二つの力の間にどのような差異があるのか——すぐに思いつくのはビオス(bios)とゾーエー(zoe)だ。古代ギリシア人たちは生命力には二つの種類があると考えた。ビオスはbiologyの語源ともなっている言葉だが、この言葉には個体的な生命力の意味がある。蝶なら蝶が羽ばたき、魚なら魚が遊泳する。生命力は個体において結晶化し、その生を表現し、謳歌する。
一方、生命力の全体性を支配している力というものもある。それがゾーエー(zoe)だ。全生物は食物連鎖という形でまるで一つの巨大な多様体のようにして生きている。土の中に微生物が生きていなければ植物は存在しないし、植物が存在しなければ当然のことながら動物もまた存在することはできない。この生命の連鎖運動はビオスが持った個体化を支える力とはある意味対極的な力となっている。なぜなら、生態系全体の流動を守るために個体性が滅びることもあれば、まだ、全体性を浸食していこうと渇望する個体性もある。人間(ホモサピエンス)などはその典型的な例と言っていいだろう。
ヌーソロジーが展開する思考図式からすると、太陽が持った生命力がビオスで、月が持った生命力がゾーエーである。その意味で、太陽-地球間への月の割り込みである日食はビオスの力を無効にしようと介入してくるゾーエーの力と深い関係を持っている。つまり、日食は生命の全体性への回帰の扉の出現とも言えるものだ(下図1参照)。
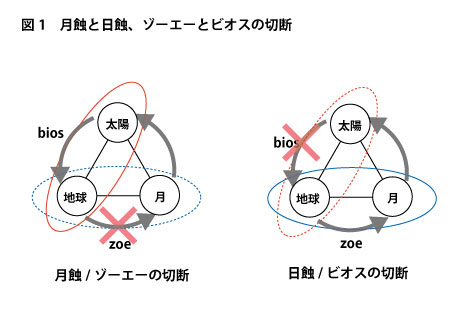
生物において個体化を進める力のソースはおそらく太陽にある。人間においてはそれは理性(アポロン的なもの)として現れてくるのだが、この理性は医学における身体観や政治学における身体観を例に挙げるまでもなく、生命を物質や社会といった枠組の中で外部操作的に扱うことに長けている。こうした局面で思考されている身体の力はすべてビオスに負うところが大きいのではないか。国家が個体の誕生や死を登録、管理し、バイオテクノロジーが個体の遺伝子を操作、制御する。人間はビオスの力を利用し、それによって力は個体性の名のもとに囲われ、生命という大義名分のもとに人工飼育されるのだ。
月が太陽を食らうという現象は、こうしたビオスの力から逃走しようとするゾーエー側からのカウンター(対抗)と考えられる。地球-月-太陽というトリニティー構造の中で生命エネルギーを円滑にを循環させていくためには、ビオスがもたらす個体化や制度化というエネルギーの萎縮を再度、原初的生命力であるところのゾーエーへと刷新していく必要があるからだ。個体へと凝縮を行ったものは、また、全体へと解放されなければならない。それは生と死、エロスとタナトスの間に働く呼吸でもある。生命エネルギーが持った全体性への放流は地球と太陽、つまり、物質と精神の癒着を無効にし、月に象徴される身体そのもののが持った力を甦らそうとする。身体自身は人間の理性には統御不能な無意識の海であり、そこにはデュオニソス的な情動力が渦巻いている。ベンヤミンの言葉でいえば神的暴力の坩堝である。
グローバルスタンダードの名のもとに日ごと画一化していく社会に対して、絶えず謀反を起こそうと企てる異端分子的エネルギーはその意味で言えば、神的暴力の力でありゾーエーから迸り出るものだ。個体性にとって全体性は極めて危険な暴徒であり、反対に、全体性にとって個体性は無秩序のカオスを作り出す要因でもある。僕ら人間の生命力は今、ビオスとゾーエーの狭間で大きく揺らいでいる。太陽の時代は終わった。といって月の時代を標榜するのは退行である。のぞむべくは、日食という扉を通して、月と太陽を結ぶルートを敷設する必要があるのだ。そこに流れているものはビオスでもゾーエーでもない、第三の生命力である。その力を目覚めさせるためには、僕らは地球の結び目をほどかなくてはならない。地球の結び目とは物質のことである。
By kohsen • 10_その他 • 13