内面と外面

　●モノから広がる空間と観測者から広がる空間は全く違うもの
　さて、これから次元観察子ψ5とψ6の球空間について、その幾何学的な構造を大まかにチェックしていってみたいと思います。前回の図1からも推測できるように、ψ5の球空間の方は現実として見える前方向（光速度状態として奥行きが無限小の長さにまで潰された前方向）が回転によって作り出した球空間、ψ6の球空間の方は想像的「後」方向がその回転によって無限大の広がりを作り出している球空間ということになりますが、幾何学的にこの両者はどのような関係で表すことができるのでしょうか。まずは、NC上でこれら両者のカタチの成り立ちを見てみることにしましょう。
　NC上で観測者の前を表すにはいろいろな方法がありますが、最も分りやすいのはモノの背後側（矢印a）とモノの手前側（矢印b）を合わせ持った場所を「観測者の前方向」と見なすことでしょう（下図1）。結果的に、この矢印aと矢印bをつないだ矢印を観測者を中心に3軸で回転させた空間がψ5の球空間ということになりますが、これだとψ3〜ψ4の球空間との区別がつきにくいので、ここでは次のような別の見方を取ることにします。

　モノの背後方向を表していた矢印aは、見方を変えれば、観測者の後方に突き刺さってくるような矢印でもあることが分かります。そこで、この矢印aを右側の球体C側の方に移動させて表現し、矢印a’とします。するとψ5の球空間を作るためには矢印bと矢印a’をつないだ矢印、つまり、右側の球体Cの直径幅の矢印をそのまま3軸回転させればいいことが分かります。同様にψ6は人間の内面側なのでψ5の球空間の直径を作っている矢印とは反対方向の矢印を直径として、そのままこの直径を回転させたときにできる球空間と考えるといいでしょう（下図2参照）。

　このように、NC上での次元観察子ψ5〜ψ6の球空間の成り立ちを見て言えることは、モノから広がる球空間（次元観察子ψ3〜ψ4）と観測者から広がる球空間（次元観察子ψ5〜ψ6）は、互いに全く次元が違うものだということです。3次元認識に捕われた見方で見てしまうと、モノも観測者も同じ物体にしか見えませんから、それらの回転が作る空間も観察子で言えばψ3〜ψ4レベルの空間となってしまいます。しかし、人間の外面（観測）という概念が考慮されると、観測者から広がる球空間はモノから広がる球空間に比べてその半径が2倍になっていることが分かってきます。NCで言えば、ψ3の球空間の半径は上図に示した点Ｏと−∞を結ぶ線でしたが、ψ5の半径は＋∞と−∞を結ぶ線になっているということです。

　この2倍の半径の意味は結果的に、観測者から広がる空間がモノから広がる空間を無数持ち合わせた球空間になるということになって反映してきます。これは実際に確かめてみればすぐに分かります。「わたし」がグルっと回ってどこに視線を向けようが、その視線上の一点には、その一点を中心とするようなモノから広がる空間を想定することができますよね。言い換えれば、次元観察子ψ5〜ψ6という球空間はそれぞれが無数のψ3〜ψ4の集合で構成されているということなのです。
　さて、おそらく上でのNC上でのψ5とψ6のイメージは分かりづらかったと思いますので、ここでもう一歩突っ込んで、次元観察子ψ5とψ6の球空間がどのようなカタチを持っているかを調べてみましょう。ψ5の球空間の中心点はNCを見て分るように＋∞と−∞の重合点になっています。これは観測者の位置そのものです。この重合のイメージを取りあえず実際の空間上で作ってみることにしましょう。すると、ちょっと奇妙な描像ですが、それはおおよそ次のようなイメージになってきます（下図3参照）。

　目の前にモノがあります。その背後に遥か彼方まで延びる無限の長さの直線があります。そして、その直線が無限遠点（−∞）に達したところに自分がいます。しかし、そこに見える自分は自分の後頭部です。このことを想定した上でグルっと回ってみましょう。すると、回っても回ってもその視線の彼方にやはり自分の後頭部が見えることになります。つまり、次元観察子ψ5という球空間は観測者が知覚球面を形作ったときには、その球面上のどの方向にも観測者自身の後頭部が見えるような構造になっているということです。はて、はて？何のこっちゃ？——つづく

　●第二のモナド
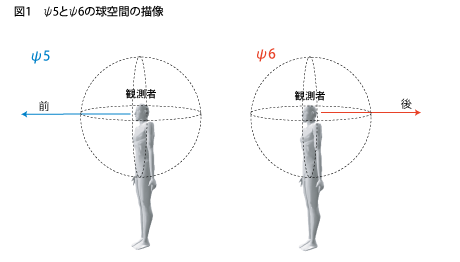
　次元観察子ψ5～ψ6の描像は、その描像だけとっていえば極めて簡単なものになります。ψ3～ψ4でモノが果たしていた役割を、今度は「わたし」の身体に置き換えればいいだけです。つまり、『人神/アドバンストエディション』にも書いたように、わたしの身体の前方に延びていると想定される線をグルっと回転させ、そこに生まれている線を綜合したところに概念化される球空間（正確には3軸での回転を行なう必要があります）、これが次元観察子ψ5となります。そしてその反対に、わたしの背後方向に想像されている線を同じくグルっと回転させたところに概念化されている球空間、これが次元観察子ψ6となります（下図1参照のこと）。しかし、次元観察子のψ3とψ4を「等化」した空間が、なぜわたしの身体の周囲の空間となるのでしょう？まずは、その理由について少し説明してみます。

　ψ3とψ4の球空間が等化されるためには、ψ1～ψ2をψ3として等化したときと同じように、その形作る球面が外面=内面、内面=外面というような捻れを持たなくてはいけません。しかし、ψ3とψ4の球空間を限界づけているところは無限遠点ですから、単なるモノの表面が作り出している球面のイメージを反転させてイメージさせても等化には至りません。無限遠点自身自体が内面と外面を捻るような捻れを持っている必要性が出てくるのです。さて、このような捻れを意識に形作るにはどのような思考を展開すればいいのでしょうか。

　まずは、ψ3の球空間の内壁をイメージしてみましょう。これはモノを原点として広大な広がりの果てに「見える」天球面としてイメージされるはずです。そのとき、その天球面を主体の位置と見なせば、それはもう無限遠に到達したことになると考えます。なぜなら、単なる物質的な運動のイメージではどうしても到達することのできなかった「無限遠」という位置に「主体の位置」という差異をはめ込んで3次元の限界を飛び越えたからです。この措定を3次元という概念が持つ同一性からの跳躍と考えましょう。そして、以前お話したように、この－∞への方向の無限遠が形作る球面をそのまま「点」と見なして下さい。言葉遊びにすぎませんが、実のところ転すれば天とは点でもあるということです。なぜ天を点と呼べるのかというと、ψ3の球空間の内壁上のどの方向を取っても「わたしの身体の前方」という意味ではどこも同じ方向になっているからです。身体の側から主観的に世界を見た場合、それは、わたしの「前方向」という直線上の「1点」でしかないというということが分かります。例の面点変換という概念です。ここは少々分かりづらいかもしれませんが、僕らは「前」でしか世界に接してないのだという考え方をしているわけです。

　さて、ここで、このとき見えている天球面の「裏面」について考えてみましょう。これはψ3の球空間の内壁（人間の外面）の裏側に当たる部分ですから、ψ4の球空間の内壁（人間の内面）に当たります。人間の内面であるψ4の球空間の内壁は、観測者にとっては自分の背後方向のはるか彼方に想像されているものでした。そして、この方向は「後ろ」ですから、この内壁は決して「見ることができない」天球面になっています。しかし、たとえ見えなくてもこの天球面は「身体における後方」という意味で、さきほとの「前方向」同様に、主観的な空間に立てばどの方向をとっても「後ろ」という名の同じ方向性だと考えることができます。

　このように考えてくると、結局のところ「ψ3とψ4を等化している空間」というのは「身体における前方向と後方向とを等化している空間」と同じ意味だということが分ってきます。前を後にする方法は簡単です。今度は観測者自身が自分の主観的な空間の中でグルっと自転すればいいだけです（ここで、身体を自転させても前は前だろ、と考える人がいるかもしれません。それについては後でまた説明します）。このとき、自転の軸は当然、x、y、zの三つが出てきますが、この三軸を使って自転したときに形成される空間の綜合が次元観察子ψ5ということになります。

　このことは何を意味しているかというと、主観的な空間において認知されている身体の位置というのは、実際は、客観的な空間における＋∞としての無限遠点と－∞としての無限遠点の重合点、つまり、ψ3とψ4が形作っている球面の捻れの位置そのものになっているということを意味しています。そして、観測者自身の自転によって形作られているこの球空間（これを知覚正面と知覚背面を等化した球空間という意味でこれから知覚球体と呼ぶことにします）の奥行き方向もまた知覚的事実として一点同一視されていて長さというものをほとんど持っていないわけですから、人間の内面認識においてはミクロの微小空間内に点状の微粒子状の存在として現れることになるはずです。

　次元観察子ψ5が知覚球体であることが分ると、次元観察子ψ6はその反転空間なわけですから、自ずとその正体を明らかにしてきます。そうです。冒頭にも書いたように、それは観測者の背後方向への延長を半径とする球空間です（ψ5同様、x、y、zの三軸で回転したときの綜合による球空間と考える）。しかし、こちらの球空間は無限遠が視覚としては生じてはおらず、想像上、概念化された正体不明の遠い遠い場所になっているので、文字通り、延長概念によって象られた広大な球空間になってしまいます。これが正式な意味での局所的時空です。

　皆さんも、以上の説明を頭に入れて、実際にその場で回転して次元観察子ψ5とψ6を意識に構成して見るといいでしょう。大きな大きな宇宙空間の中心に、小さな小さな粒のような宇宙空間がくるくる回りながら入り込んでいるのが容易に感覚化されてくるはずです。――つづく