2月 28 2014
シリウスファイル解説
シリウスファイルの紹介が思いのほか好評だったようなので、若干のイメージが作れるように少しだけ解説しておきます。
コ : 水素原子とは定質のことですか。
オ : はい、そうです。内面性における付帯質の覚醒を生み出したときに存在するものです。
【解説】
僕の質問にある「定質」とは「人間の定質」のことで、この言葉には文字通り「人間という存在を定める力」という意味があります。人間の個体意識を生み出すために働いている無意識のシステムの全体性の力のことを指していると思って下さい。一方、個体意識として生み出されている方の力はOCOT情報では「性質」と呼ばれており、「人間とは性質が生まれている状態」として定義されています。定質=人間の無意識側で働く主体、性質=人間の意識側で働く自我、ととりあえず覚えておくのがいいでしょう。
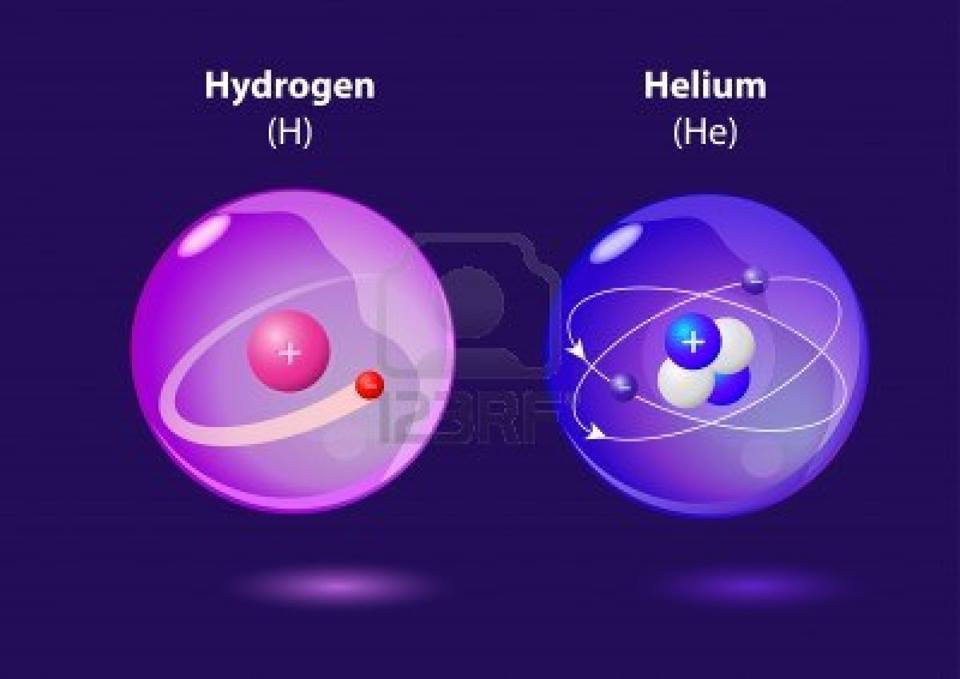
ここでいう「内面性」とは意識が能動的に働いていく世界、つまり創造空間のことと思って下さい。付帯質とは人間が時間と空間と呼んでいるもののことでもあり、さきほどの〈性質〉とほぼ同じ意味です。「付帯質の覚醒」とは人間の自我意識が時間と空間という形式を離脱して、ダイレクトに創造空間の中に侵入していくことを意味しています。OCOT情報は人間が時間と空間と呼んでいるものは人間の自我とほとんど同じものと見なしているようです。無意識構造は空間の多重構造の中で組織化されているのですが、その全体性は奥行きを通して〈収縮〉しており、時空上では僕らが水素原子と呼んでいるものに見えているということです。
コ : ということは、水素分子とは定質の対化のことですか。
オ : 力の交差の方向性。中和の交差が起こったときに定質の対化となります。つまり、次元の対化です。力の交差が反対側を向いているということ。
「力の交差の方向性」とは自己と他者、互いの無意識構造が表裏を捻り合って交わっているということを意味しています。自己と他者の無意識構造が表裏一体でメビウスの帯のようかたちで繋がり合っているということ。ここには、自己側の無意識が他者側の意識を活動させ、他者側の無意識が自己側の意識を活動させる、といったような捻れの関係が潜んでいます。魂の世界では自己と他者が互いの無意識を支え合っているということです。
「力の交差が反対側を向いている」とは、人間が受け取っている物質の表象(ものの見え姿)と表象を送り出している力の関係性のことを言っています。水素分子とは、その意味で言えば、自己と他者に表象を送り出しているもの同士が一つになっている場所のことです。水素分子にはオルト水素とパラ水素という二つの種類がありますが、捻れが見えているものがオルト水素で、見えていないものがパラ水素として現れています。
コ : ヘリウム原子とは性質のことですか。
オ : はい、性質と反性質が性質の対化の意味を持ちます。
コ : 水素原子に中性子がないのはなぜですか。
オ : それは対化の交差が内面を持てないという意味です。中性子は力の交差を持つための次元ですから、それがないということは上次元に関与する力がないということです。
【解説】
ヘリウム原子は基本的には陽子が2個、中性子が2個、電子が2個で成り立っていますが、これは水素分子が付帯質の力を付随させているものという解釈ができます。単に無意識側の力だけではなく、人間の自我意識側をも含んでいるということです。原子の世界では精神側(無意識側)の力が陽子、付帯質側(無意識が相殺されたもの)の力が中性子として投影されています。ですから、水素分子が定質の対化ならば、必然的にヘリウム原子は「性質の対化」という言い方がなされるわけです。
「対化の交差」とは精神と付帯質の交差を意味しています。精神の付帯質への交差が人間の意識に外在認識を作り、付帯質の精神への交差が内在認識を作っています。単純に物質世界とこころの関係と言っていいでしょう。中性子がないということはダイレクトにいえば自分を顧みる力がないということです。その意味で言えば、中性子とは人間の心に対応すると考えられていいと思います。「上次元に関与する力がない」というのは創造空間を構成する実体側に方向を持つことができていない、といったような意味です。心が人間の意識をほんとうの宇宙に方向付けているということ。







6月 20 2014
パウリ行列、学習のススメ
今日の話は少し難しいかもしれません。
ラカンのシェーマLやメルロポンティのキアスムに共通する「捻れの構造」が物理学の中に現れたものがSU(2)の生成子となるパウリ行列です。無意識の構造を能動知性として追跡していくに当たって、このパウリ行列が提示する回転のイメージは最重要なものとなってくるでしょう。
このパウリ行列による回転は物理学的事実として無限小世界にあると想定されているものなのですが、この回転は普通の3次元空間における回転とは違って、回転によって描かれる円環がメビウスの帯のような形を持っています。つまり、円環の内部側と外部側が捩じられたような構造を持っているのです。「捻られた」ということは、ここでは内部=外部、外部=内部というパラドクスが成り立っている、とも言えます。
僕らが親しんでいる3次元空間ではこうは行きません。たとえば、球体をイメージしてみて下さい。球体は球面を境として内部と外部をきれいに分離しています。しかし、パウリ行列が作り出している球空間は球面上の対極点(互いに180度反対側に位置する点の組)が繋がっているために3次元球面という形をしています。3次元球面というのは2次元球面の3次元版のようなものと考えればいいでしょう。
2次元球面は2次元平面における直交軸x,yのそれぞれの端と端をつなげることによって出来ます。これと同じでx,y,,zそれぞれの軸を円として繋げはこの3次元球面という形が出来上がります。
しかし、通常の3次元認識ではこの形をイメージすることはできません。それは3次元認識では無限遠方が永遠に開いた方向としてイメージされており、無限にたどり着かない位置としてしか描像できないからです。ですから、3次元球面の形を認識に浮上させるためには、無限遠点を開いたものではなく、文字どおり閉じた「点」として描像することが不可欠になってきます。
昨日、「無限遠点とは観測者自身の意識の位置である」といったような話をしました。そして、それが分かったときには奥行きは虚軸になるとも。奥行きが虚軸化すると大きさはまったく意味を持たない空間に入ります。実は、その空間が僕らの視覚空間なのです。大きさが支配している空間は触覚空間です。つまり大きさというのは僕らが「触る」という感覚に準じていて、決して「見る」ということには準じていないということです。
そうやって大きさの空間から差異化された奥行きはもはや時空上の存在ではなく、一点同一視のもとに無限小空間に一気にワープしてきます。奥行き方向自体に距離が見えないのもそうした構造が背景にあるからだと考えることができます。このとき、奥行きは射影線そのものになっており、それはもっと言えば、光子のスピンとも言っていいものに変貌してきます。光の中では時間も空間も存在しません。つまりは、光とは見るものと見られるものをダイレクトに一致させている働きでもあり、哲学の言葉でいえば実体形相(イデア)とも呼べるような存在なのです。
幅の空間認識から奥行きの空間認識へと移行することによって認識するものと認識されるものとが一致する世界に入ることは、「包みつつ包まれるもの」というライプニッツの逆モナドへの移行を表わしているとも言えます。幼児が母親と視線を交ぜ合わせながら世界を徐々に構成していく無意識の見えないシステムがこの逆モナド化した空間の奥に美しい構造として存在しています。
その構造の中核にあるのがこのパウリ行列だと考えるといいでしょう。このパウリ行列は素粒子世界の最も基礎的な枠組みを担っているのですが、今まで話したような文脈で思考されてくる素粒子の世界は、物理学者たちが言うように単なるエネルギー粒の相互作用といった貧相なイメージで描かれるものではなくなってくることが分かります。それらは実のところ、僕たち自身の魂のネットワークが張られている空間と言ってもいいようなものとしてイメージ化されてきます。
さて、この空間に入っていくか、行かないか——それは、あなた次第です(笑)
このパウリ行列に関してはS博士が痛快なほどに分かりやすい解説をしてくれています。いずれヌースアカデメイアでもDVD化する予定ですが、とりあえずはSさんのサイトでの解説を参考に。回転自体の解説は次のファイルの14ページにあります。
http://newton2013.web.fc2.com/math/gyouretsu3.pdf
数学が苦手な人は最初は何が何だか分からないと思いますが(僕もそうでした)、一つ一つ丁寧に理解していけば、「なーるほど、こんなイメージだったのか」というのが分かってくるはずです。もちろん、そこでは「奥行き(持続)と幅(延長)の区別」をしっかりとつけるというトランスフォーマーのたしなみが前提とされますが(笑)
パウリ行列のイメージはいきなり「分かった!!」というよりも、発酵食品のように徐々に醸成されてくるものです。このイメージが醸成されてくると、今まで3次元を中心として働いていた意識が、あたかもお風呂の栓を抜いたときのように、猛烈な勢いで渦を巻いて自分自身の内在空間の中へと流れ込んでいくような感覚が湧き上がってきます。そして、その先に内在に潜む他者の横顔がチラリと見え出したりもするのです……
By kohsen • 01_ヌーソロジー • 0 • Tags: パウリ行列, メビウス, メルロ・ポンティ, ライプニッツ, ラカン, 佐藤博紀