6月 7 2016
アリアドネの糸をたぐって
古神道の熱波がひと段落して、現在は頭を物理学モードに切り替えている最中。思考しているのはいつも同じものなので、同じ美しい女性をアングルを変えて見ている感じだね(笑)。
人間の無意識構造と素粒子構造の関係性を思考していくにあたって、奥行きと幅をそれぞれ虚軸と実軸に見立てることがいかに重要かは何度もつぶやいてきた。未だ物理学は複素数で示される空間を素粒子記述のための単なる数学的道具としてしか見ていないが、ヌーソロジーの思考からすると、それは確実に潜在的なものの活動場の数学的表現になっている。
わたしたちが知る時間と空間の世界は、この自他それぞれが構成している複素空間の統合から現れてくると考えいい。自他においては本来、虚軸(奥行き)と実軸(幅)が互いに逆の関係で構成されているのだが、それらをそれぞれ共通の奥行きと幅にまとめるような運動が複素空間自体の中で起こっているということだ。
自他それぞれの奥行きと幅を交換するためには互いを捻る必要があるが、この捻れを含んだ回転運動がSU(2)―複素2次元空間におけるスピノルの回転―だと考えるといい。この回転によって、自己の奥行きと幅が他者のそれらと同一化する場所が生まれ、そこに時間と空間が出現してくるような仕組みになっている。
このSU(2)構造は意識の上では左方向からの視線の介入と、それに伴う奥行きの幅化をもたらす。「横から見ると奥行きが幅に見えるでしょ」というやつだ。自己本来の奥行き=虚軸を持続軸として考えるなら、このとき起こる空間の二重化が非局所と局所の重なりを目の前の空間に与えてくることになる。要は見ている空間と見られている空間の二重化だ。わたしたちの目前にはミクロの素粒子世界とマクロ世界が同時に重なっている。このことは執拗に何度でも言わなくてはならない。
この二重化にはっきり気づくことをヌーソロジーでは「顕在化」と呼んでいる。今まで無意識の中に沈んでいた内在性としての持続空間が認識の対象として浮上してくるということだ。
噛み砕いて言うと、対象側から働きかけてくる空間は局所的な時間と空間の世界だが、身体側から働きかけている空間は非局所的な複素空間だということ。
この二つがはっきりと見えてくると、今まで曖昧な表現でしか語ることのできなかった、主客一致の意識空間を科学的な明晰性を持って思考上に明らかにしていけるようになる。言い換えれば、物理学で用いられている様々な数式を魂の構造表現として読み取っていくことが可能になるということだ。
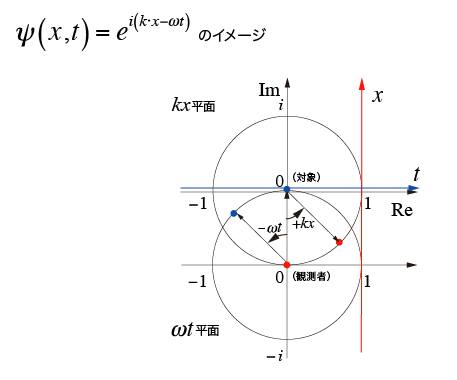
例えば自由粒子の波動関数Ψ(x,t)=e^i(kx-ωt)の意味をこの二重の空間性から考えてみよう。
Ψ(x,t)をΨ(x,t)=e^ikx×e^-iωtというように変数分離して考えると、波動関数が空間を巻き込んだ回転e^ikxと時間を巻き込んだ回転e^-ωtの合成からなっていることが分かる。これを図で示すと下図のようなイメージだ。
細かい説明は省くが、この二つの回転は何を意味しているか結論だけ書くと、観測者の持続が時間と空間上に位置を規定しようとしてる活動を表している。サルトルのいう想像力と言ってもいいだろう。観測者が持続空間を使って対象の周りに視点を巡らしている様子をここには表現している。
つまり、観測者が想像的に対象の周りを公転しながら、自分自身は自転しているということだ。これによって、対象をいろいろな角度から見た像が意識に想像的に構成される。e^ikxが対象周りの公転に対応し、e^-iωtが観測者自身の自転に対応すると考えるといい。ちょうど、地球の周りを月が裏を見せずに回っているようなイメージだ。
これらのことから自由粒子の波動関数Ψ(x,t)とは、わたしたちが時間と空間の中である一つの位置の認識を行うための無意識構造だということが分かる。要は、量子力学において物理学者たちは「観察している自分自身を観察しようとしている」わけだ。
この波動関数Ψ(x,t)の解釈を基本として、ヌーソロジーは物理学に登場する様々な数学的、幾何学的概念を無意識の構造として読み取っていく作業を行っている。そこからはっきりとわかったことは次のようなことだ。
素粒子構造はわたしたちの無意識を霊的世界へと方向づけている。この構造がなければわたしたちの意識も存在しない。時間と空間の世界さえその構造のほんの一部にすぎない。
こうした世界観へと早くシフトしたいものだ。わたしたち自身が素粒子なのであり、それが分かってこそ、初めて本当の宇宙が見えてくる。
素粒子とは人間に唯一与えられたアリアドネの糸だ。この糸をたぐって迷宮から出よう!!







8月 3 2016
量子力学は天と地をつなぐ剣の知識となるべき―「僕らのヌースレジスタンス」
素粒子は円環的、時空は直線的といつも言ってるけど、この関係を分かりやすく例えると、巻尺とそこからスルスルと延びてくるメジャーの関係に似ているね。つまり、素粒子というのは物質的な対象ではなくて、時間と空間を巻き込んだ球体のようなものと思うといいよ。
その巻き込みの様子が数式として表されているのが波動関数(平面波の式)のψ(r,t)=Ae^i/h'(p・r-Et)というヤツ(以降h’=ディラック定数)。空間がr(=x,y,z)。時間がt。ムッチャ難しい式に見えるかもしれないけど、基本はe^iθという複素平面上の単位円における回転。今言った時間と空間を巻き込んだ円がこの式で表されていると思うといい。
素粒子を時空の中の対象と見なせば、それは物体のように運動するものになってしまうよね。運動すると、そこには運動量やエネルギーというものが生まれるわけだけど、運動量やエネルギーといった概念は言うまでもなく、時間とか空間があって初めて概念化できている。
でも、素粒子は時空上にあるのではなく、時空を巻き込んでいるわけだから、通常の物体のように時間と空間の中を運動しているわけじゃない。だから、ダイレクトに運動量やエネルギーを導き出すのも無理。
こうした理由から、量子力学では運動量やエネルギーといった物理量が演算子に置き換えられてしまうんだね。
演算子というと難しく聞こえるかもしれないけど、ぶっちゃけ、巻き込まれた時間と空間を巻尺の中から再びメジャーとして直線的に引っ張り出すということ。このときの操作が数学的には「微分」に対応している。これは円に接線を引くイメージと考えるといい(下図参照)。
で、運動量を出したかったら波動関数Ψに運動量演算子-i/h’∂/∂rというのを作用させる。これは「Ψを空間rで微分して-i/h’をかけよ」っていう指令のようなものだと思えばいい。
すると、ψ(r,t)=Ae^i/h'(p・r-Et)の肩に乗っかっている()の中のp(運動量)がe^iθの前に飛び出してきて、実数値として弾き出されてくる(係数Aは確率振幅と呼ばれるものだけど、ここでは考えなくていい)。
エネルギーpだったら演算子はi/h’∂/∂t、つまり時間で微分してi/h’をかけなっせ、そしたら、Eが前に実数値として飛び出してきまっせ、ということになる。
つまり、時間と空間を共に巻き込んだ巻尺から、運動した空間を引っ張り出すか、運動にかかった時間を引っ張り出すか、それによって粒子の運動量とエネルギーが決められるってことだね。
普通、物理学者たちはこれを単なる数学的手続きとして考えていないので、すんなり素通りしちゃうわけだけど、思考する人はここから「量子の世界がこんな仕組みを持っているのはなぜか?」と考えなくちゃいけない。空間並進(移動)がそのまま運動量になって、時間並進(経過)がそのままエネルギー? どういうこっちゃ、これ? と考えるわけ。
観測問題などもあって、量子が単なる対象ではないことはもう分かってる。勘のいい物理学者たちは、それは役者でもあり観客でもあるということをすでに知ってはいる。。つまり・・・そう、観測するもの自体が観測されているということなんだね。空間をこれだけ移動したという認識、時間がこれだけ経過したという認識。。それが量子の運動の正体じゃないかってこと。
となれば、この内的認識力自体が(これは物理的力ではないよ)が時間と空間いう場所に表出してきた状態が素粒子が持つ物理量としての運動量やエネルギーとして、つまり、対象として観測されているってことになる。ただし、ここで-i/h’やi/h’(微分演算子の前についている係数)というフィルターを通して実数化するというズルをしているけどね。
この-i/h’やi/h’の正体は他者と関係していると思うといいよ。認識という内在性を客観世界側に持ってくるために他者と共有できる空間に翻訳しているんだ。これが実数の場だね。
だから純粋な複素数量(「量」という言い方は的確じゃないけど)というのは、僕らの内在性の中に眠る持続空間の力だと考えるといい。人間の精神と無関係な物理的客観世界なんてものはハナから存在していないんだよ。
その目で自然を見てみるといいよ。それは僕らとは無関係に外に作られてきたもんじゃない。じゃあ、一体何だ? 答えはたぶん一つしかないよね。素粒子が僕らの内在なんだから、素粒子で作られている自然も僕らの内在なんだよ。僕らの内在の奥の奥にこの自然を生成させている未知の空間があるんだよ。僕らはせっかく想像力を持っているんだから、そろそろその空間に向かってイメージを広げないとだめ。宇宙とは本来、その空間の中の風景を言うんだよ。
天地をつなぐ「剣」の知識によって初めて天地は同一のものとなる―古代から人間が憧れ続けてきたこの知識の獲得に向けて、今、新たに開き始めた奥行きの空間=剣の中に皆んなで入って行こうよ。
これが「僕らのヌースレジスタンス」だ(笑)。
By kohsen • 01_ヌーソロジー • 0 • Tags: 奥行き, 波動関数, 素粒子, 量子, 量子力学