12月 19 2006
原子の基礎
 認識にモノ概念が成立するための空間構造を幾何学的にもう少しはっきりさせておこう。
認識にモノ概念が成立するための空間構造を幾何学的にもう少しはっきりさせておこう。
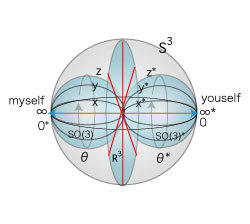
世界には無数のモノがある。今、わたしの周囲には灰皿や本やPCや外の木々や電信柱などが散在している。こうしたモノの多数性は前回示した4次元球体の構造の中でどのように対応させればよいのか——この対応を作るためには、上図のように4次元球体の内部に二つの内接する3次元球面θ、θ*をセットするとうまくいく。これら二つの3次元球面はそれぞれが自己と他者に見えているモノからx,y,z方向に広がっている3次元空間を球面状に丸めたものである。球面θでは∞側が一点で同一視され、球面θ*では∞*側が同じく一点で同一視されている。これらは言うまでもなく、自己と他者それぞれにおける主体としての位置だ。モノの3次元の並進方向は、この球面θ、θ*上のそれぞれの3つの円環の回転と考えるといい。自他がモノの並進方向を意識するとき、球面θとθ*上の円環は同期した鏡像回転を起こしている。SO(3)とSO(3)*で表されたこの二つの3次元球面の4次元方向を軸とする自転はモノから広がるx,y,z軸のすべてを観測者の「前」が等化している状態を意味する。つまり、観測者がモノの周囲をグルグルと周ったときに見える、モノの中心点とその背後方向に位置する無限遠の天球面を同一視させる運動を意味しているということだ。以上のような対応を考えれば、3次元空間上に存在するすべてのモノ(位置)を、このθとθ*の接点の位置Pに対応させることが可能となる。
以上の考察から、意識がモノ概念を形作るためには少なくともSO(4)対称性という条件が必要であることが分かるだろう。ただし、このときに概念化されるモノとは普通にいう客体としてのモノのことではないことに注意しよう。何度も言うようだが、SO(4)対称性は人間の外面に形作られるものなので、これは客体ではなく、集合主体としての役目を持っている。普通にいうところの客観的なモノとは人間の内面認識におけるモノのことであり、それはSO(4)ではなく、おそらくSO(1.3)で表されるローレンツ変換対称性として解釈されるのではないかと思う。
SO(4)対称性と言っても多くの人はピンとこないと思うので、これをSO(3)×S^3という形に書き直してその物理的意味を考えてみる。3次元球面S^3は数学的には2次元複素ユニタリー群SU(2)と同相とされる。これは複素2次元ベクトル空間上での回転群のことだ。3次元球面S^3の双方向の自転によって生じている軸を電子のアップスピンとダウンスピンとすると、SO(4)においては、この両スピンがさらにS^3=SU(2)をなぞるように回転しているというイメージが生まれてくる。これは前回も言ったように一つのモノに対する無数の他者の眼差しに相当する。つまり、無数の眼差しの一点への集中とは、特定の自己のアイデンティーを決定している電子のスピンが、モノから広がる3次元空間上の様々な位置に配位されている様子と解釈するわけだ。このようにスピンがさらに回転しているような空間は物理学ではアイソスピン空間と呼ばれる。つまり、電子のスピンは3次元球面S^3の自転軸として出現しているのだが、そういった自転軸をさらにS^3=SU(2)に沿って回転させ、それら3方向の回転をさらに一つの方向に統合しているような上位の回転軸を想像すればいい。言うなればスピンの上位にあるメタスピンのようなものだ。その軸の双方向がアイソスピンである。物理学ではアイソスピン-1/2が陽子で、+1/2が中性子とされる。
これらの文脈から陽子と中性子の実体とは何かが描像できる。一言で言えば、それは自他における「前」の総体と「後」の総体の関係だ。これはヌース理論の文脈では集合主体の原器と集合客体の原器を意味する。そして、これら両者は実のところ客観的なモノ概念と時空全体の関係となって現れてくる。つまりこういうことだ——目の前に幾ばくかのかさばりを持ったモノがある。その周囲に空間の広がりとしての時空がある。そして、それを見ている「わたし」がいる。それらをすべて概念として解釈すると、その概念のカタチがそれぞれ陽子、中性子、電子に対応していることになる。重水素を作る材料がこれで揃ったというわけだ。







1月 23 2007
差異と反復………9
あっ、忘れてた。複素平面に話が移る前に、もう一つだけ確認しておかなくてはならないことがあった。それはモノと空間の差異によって生み出される現存在の方向は大まかに言って二つある、ということだ。これは前々回話した2次元射影空間の性質を確かめてみると直観的に分かる。射影空間自体は球面上の対蹠点を同一視することによって作られるが、それは結果的に半球面のかたちをとることになる。すると、射影の方向を球面のオモテ側から取るか反対側から取るかによって、方向性が逆の二枚の2次元射影空間が生まれるわけだ。
これを実際の知覚の現場に即して言えば、物体の背景正面には方向性が正反対となる二種類のものが存在しているということを意味する。それらが何に対応するかはすぐに分かるだろう。そう、わたしの知覚正面とあなたの知覚正面である。普通の3次元認識では、この両者は同一の球空間(宇宙)の内壁のように見えているが、射影平面的(外面認識的)に見れば、それらは表裏の関係が互いに逆になっている。つまり、前回話した物体界面と同様に「わたし」と「あなた」に知覚されている天球面もメビウスの帯状に捻れの関係にあるということなのだ(上左図参照)。
実際に、モノを挟んで「わたし」と「あなた」が対峙している様子を想像しながら、この表裏の捻れを確認してみよう。すると、あなたにとっての知覚正面がわたしにとっての知覚背面(「わたし」が背中側に感じている面だという意味。「わたし」の知覚正面の裏側と考えてもよい)となっていることが分かるはずだ。要するに、「わたし」にとっての外面は「あなた」の内面になっており、それとは反対に「あなた」の外面は「わたし」の内面になっている、ということである。ヌース理論では、観察子に見られるこうした捻れを持った双数的関係のことを「キアスム」と呼んでいる。「キアスム/chiasme」とはフランス語で交叉配列(修辞法の用語)、交叉などの意味があるが、ここで用いたのは、メルロ・ポンティのいう「転換(交換)可能性/Chiasme-Reversibilite」を強く意識してのことだ。
※ポンティのキアスムについて深く知りたい方はこちらへ→ http://www.pencil.co.jp/ronbun/mashimo/index.html
ヌースでは前回も言ったように主体と客体の萌芽の場をψ3とψ4という次元観察子で表現するのだが、これは他者側からの認識も考慮すると、ψ3-ψ4、ψ*3-ψ*4というキアスムの関係で表現されることになる。つまり、自他が共棲していると思われるこの空間には内面の3次元空間が二つ、そして外面の3次元空間が二つ、合計4種類の3次元空間が重畳させられているということなのである。この空間は僕らが客観的3次元空間と呼んでいるものとは全く別物である。
それら四つの空間の意味合いは後に回すとして、今、これら相互の関係性を抽象的な位相平面で表してみるとしよう。それぞれの空間は3次元なので、それらを球面状に丸めて、そのそれぞれの軸に当たる部分を四つに分岐した軸に割り当てると、直交する二本の軸で表すことができる。縦軸は外面を表し、横軸は内面を表していると思えばいい(下図参照)。
かなり恣意的な配置ではあるが、これがヌース理論が解釈する複素平面の本質的な意味となる。つまり、複素平面とは実(内面)の3次元空間の相互反転双対と虚(外面)の3次元空間の相互反転双対の直交関係を表していると考えるのだ。この四つの空間の区別をイメージするためにはおおよそ次のような方法を取ればいい(下図参照)。
1、まず、モノの中心を原点に置き、モノの手前側の方向(わたしの後方=他者の前方)にある無限遠方をiと見なす。
2、その反対に、モノの背後側(わたしの前方=他者の後方)に感覚化されている無限遠方を-iと見なす。
3、わたしから見てモノの左方向に伸びる直線の無限遠方を+1と見なす。
4、同じく、わたしから見てモノの右方向に伸びる無限遠方を-1と見なす。
ん?それじゃ、単なる平面にしか成らないだって。その通りだ。ここでそれぞれの軸が球空間を作るように横方向と縦方向の回転を行なってみるのだ。モノを中心に絶えずモノが見えるようにして左右方向と、上下方向にグルっと球面を作るようなイメージで回ってみればいい。上下方向は体操選手でもなければ実際には回れないが、とりあえずイメージだけしてみよう。
普段、僕らは客観空間の中で空間の方向性を認識しているので、こうした四つの方向性の区別は回転の中で意味を失ってしまうと考える。しかし、身体側(知覚側)を中心に考えるとたとえグルグル回転を行なったとしても、それらの方向は決してそれら固有の意味を失うことはない。なぜなら、身体の前方はどう回転しようが常に前方であり、そこで形作られる球空間はあくまで前方の集合としての球空間だからである。後方もまたしかり。当然、左右にしても同じである。こうした考え方で空間を捉えれば、僕らはこの空間に潜む4つの三次元空間の区別をはっきりと認識することが可能になる。(ちなみに、ヌース理論では、単なる客観的な空間の3次元性を「核質」と呼び、身体を介して介して方向づけられた3次元性の空間を「反核質」と呼ぶ。くどいようだが、これらは全く違う空間である)。
ふー。これでどうにか電磁場と意識の関係の話に進めそうだ。 つづく。
By kohsen • 差異と反復 • 0 • Tags: メビウス, メルロ・ポンティ, 差異と反復, 無限遠